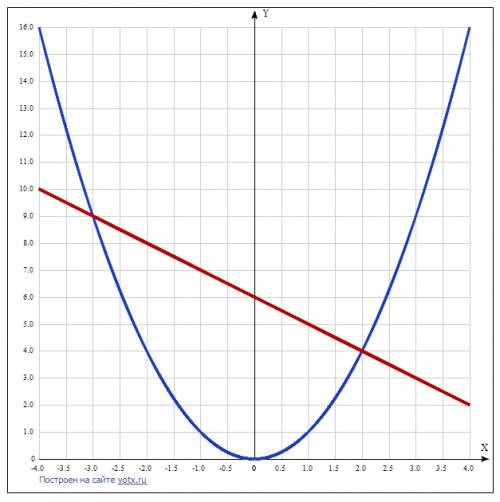
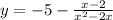
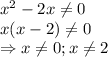
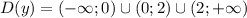
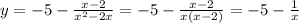
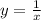, отображенную симметрично оси абсцисс и сдвинутую на 5 единиц вниз. Помним про то, что функция не определена в точках 0 и 2.
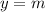представляет собой прямую, параллельную оси абсцисс, проходящую через точку (0; m). 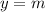не имеет общих точек с построенным графиком при 
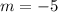(асимптота гиперболы по построению, так как сдвиг проводился на 5 единиц вниз) и при 
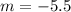(именно это значение принимала бы функция 
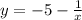в точке 2, но эта точка не принадлежит области ее определения).
Абсолютная погрешность 0,22%
20,46
Объяснение: