Ну тут всё очень просто.
Пусть х см - длина стороны BC, тогда AB (x+3) см,а площадь прямоугольника равна 28 см². Т.к. это прямоугольник, то AB=CD, BC=AD (по свойству).
Составим и решим уравнение.
S=ab (то есть произведения двух его смежных сторон)
Для нашего случая : S=x(x+3)
x(x+3)=28
x²+3x-28=0
По теореме Виета корни здесь будут -7 и 4.
-7 мы сразу можем не принимать, т.к. длина стороны это всегда положительное число.
Если x=4, то стороны BC и AD равны по 4 см.
4+3=7 см - стороны AB и BC.
ответ. 4 см и 7 см.
Теорема о медианах треугольника
Рассмотрим произвольный треугольник АВС.
teorema_o_medianah_treugolnikama – медиана треугольника, проведенная к стороне BC
mb – медиана треугольника, проведенная к стороне AC
mc– медиана треугольника, проведенная к стороне AB
O – центр пересечения медиан треугольника
A, B, C – вершины треугольника
Теорема о медианах треугольника формулируется следующим образом: медианы треугольника пересекаются в одной точке (на рисунке точка O) и делятся этой точкой в пропорции 2:1, если считать от вершины, с которой проведена медиана.
Все формулы по теме теорема о медианах треугольника:
Основные формулы
Формулы площадей
Формулы объемов
Формулы периметра
Геометрические фигуры
Объемные тела
Площадь поверхности
Тригонометрические формулы
Теоремы по геометрии
Теорема Пифагора
Обратная теорема Пифагора
Теорема косинусов
Теорема синусов
Теорема тангенсов
Теорема о медианах треугольника
Теорема о биссектрисе
Теорема о сумме углов треугольника
Теорема о сумме углов многоугольника
Теорема Чевы
Теорема Виета
Теорема Фалеса
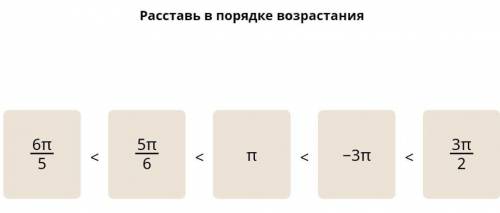
-3П; 5П\;6; 6П\5;П;3П\2
Объяснение: