Заметим, что ![x^{3}=3+[x]](/tpl/images/1164/1538/40715.png)
, то есть 
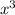— целое число. Это означает, что ![x=\sqrt[3]{m},\; m\in\mathbb{Z}](/tpl/images/1164/1538/11b9e.png)
, где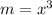 
; Имеем: ![m=3+[\sqrt[3]{m}]](/tpl/images/1164/1538/2e8de.png)
; Теперь надо отметить, что число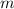 
лежит между двумя кубам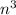и: 
и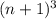 
; Пусть 
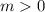. Тогда ![[\sqrt[3]{m}]=n](/tpl/images/1164/1538/dff55.png)
; Но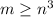 
, тогда 
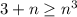. Решим это неравенство:
Докажем, что для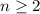 
решений нет. Действительно, касательная к 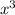в точке 
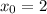имеет вид 
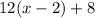; Более того, для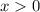 
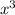выпукла вниз (
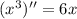); Значит, для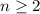 
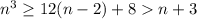; Осталось проверить значение 1, которое подходит.
Значит,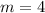 
и ![x=\sqrt[3]{4}](/tpl/images/1164/1538/c0cd9.png)
; Если 
, то аналогично ![n=[\sqrt[3]{m} ]](/tpl/images/1164/1538/2984a.png)
и неравенство уже справедливо для всех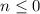 
; Но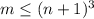 
поэтому 
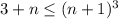, что не имеет решений при отриц. 
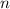. Здесь аналогично. Рассмотрим касательную в точке 
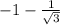; Тогда она имеет вид: 
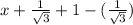; По выпуклости вверх на интервале 
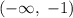можно записать неравенство для 
: 
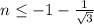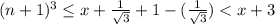; Тем самым, остается проверить значения 
и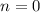 
. Они не подходят, откуда заключаем, что решение единственно.
ответ:
1. 1) 7(x-2)(x+2)
2) 3a(a-6)(a+6)
3) (x+y+8)(x+y-8)
4) 3a²(5a - 1)²
5) 3(2m - 3n)(2m + 3n)
2. x = 0; -2; +2
Объяснение:
1. 1) 7x² - 28 = 7(x² - 4) = 7(x - 2)(x + 2)
Выносим 7 за скобки. Дальше - формула сокращенного умножения.
2) 3a³ - 108a = 3a(a²-36) = 3a(a-6)(a+6)
Выносим 3a за скобки. Дальше - формула сокращенного умножения.
3) x² + 2xy + y² - 64 = (x + y)² - 8² = (x+y+8)(x+y-8)
2 формулы сокращенного умножения
4) 75a⁴ - 30a³ + 3a² = 3a²(25a² - 10a +1) = 3a²(5a - 1)²
Выносим 3a² за скобки. Дальше - формула сокращенного умножения.
5) 12m² - 27n² = 3(4m² - 9n²) = 3(2m - 3n)(2m + 3n)
Выносим 3 за скобки. Дальше - формула сокращенного умножения.
2. 7x³ - 28x = 0
Выносим 7x за скобки.
7x(x² - 4) = 0
Или 7x = 0, или x² - 4 = 0
x = 0 (x-2)(x+2) = 0
x = -2, или x = 2
3
Объяснение:
-5,78+5 1/9-0,22+3 8/9=-6+9=3