a)y(наиб)=2
y(наим)=-2
b)y(наим)=-29
y(наиб)=31
Объяснение:
a)
1)Находим производную функции :
f'(x)=3x^2-3
2) Приравниваем производную к 0 ( находим нули производной):
3x^2-3=0 --> x=1
x=-1
3) Промежутку принадлежит только точка x=1 , поэтому значения функции на концах и в точке 1:
f(0)=0
f(1)=-2-наим
f(2)=8-6=2-наиб
б)
1)Находим производную функции :
f'(x)=3x^2+3
2) Приравниваем производную к 0 ( находим нули производной):
3x^2+3=0 --> решений нет , значит наибольшее значение достигает правом конце отрезка [-3;3] , а наименьшее - в левом:
3) f(-3)=-27-3+1=-29
f(3)=27+3+1=31
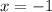
Объяснение:
Для того, чтобы определить точку максимума функции нужно проделать три шага.
1 шаг. Найти производную функции.
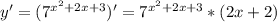 *ln(7)
*ln(7)
2 шаг. Приравнять полученную производную к нулю.
Так как показательная функция никогда не может равняться нулю, приравниваем к нулю правый множитель.
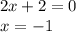
3 шаг. Исследовать полученную точку на предмет максимума и минимума.
--------------------()---------------------> х
- -1 +
Вообще-то, у нас получилось, что 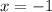 это точка минимума, т.к. знак меняется с "-" на "+".
это точка минимума, т.к. знак меняется с "-" на "+".
И, если внимательно посмотреть на функцию, то абсолютно очевидно, что у нее нет точки максимума, т.к. показательная функция с основанием больше 1 (7 > 1), следовательно она возрастающая, а в степени квадратичная функция с коэффициентом a > 0 (1 > 0), которая устремляется ветвями своей параболы в бесконечность и тоже является возрастающей.
ответ на фотографии :)))