Выразить вектор через базис системы векторов Добрый вечер. ! Задание: Найти какой-нибудь базис системы векторов и выразить через этот базис остальные векторы системы:
Мои действия (фото): Я привел матрицу к ступенчатому виду методом Гаусса, нашел базис: a1, a2, a3. Но встал в ступор. Как выразить теперь через этот найденный базис a4 ?
Пусть х — количество учеников, которые были в комнатах по 4 человека. Тогда х/4 — количество четырёхместных комнат (х учеников расселили в комнаты по 4 человека). Количество человек, живших в трёхместных комнатах — 71-х (т. к. все, кто не жил в четырёхместных комнатах, жили в трёхместных). Тогда количество трёхместных комнат — (71-х)/3 (71-х человек расселили в комнаты по трое). Так как всего комнат 20, и они были только трёхместные и четырёхместные, получаем:
20= (20 комнат — это все комнаты, и трёхместные, и четырёхместные).
Решим получившееся уравнение:
20=
20 =
20=
Умножим обе части на 12:
240 = 284 - х
х = 284 - 240
х = 44
ответ: 44.
Примечание: чтобы убедиться в правильности ответа, можно сделать проверку:
Если в комнатах по 4 человека жили 44 ученика, всего четырёхместных комнат было 44/4=11.
Т. к. всего комнат 20, то трёхместрых комнат 20-11=9 комнат. Т. к. все они заполнены, в них должно жить 9*3=27 учеников.
После того, как 44 ученика поселили в четырёхместные комнаты, осталось 71-44=27 детей — именно столько должно было жить в трёхместных комнатах.
-2х²+10х-8≤0 Разделим для удобства на -2 (знак поменяется) х²-5х+4>=0 Приравниваем к нулю х²-5х+4=0 a=1 b=-5 c=4 Т.к. a=1, можно применить теорему Виета: x1 + x2 = -b = 5 x1 * x2 = c = 4 x1 = 1 x2 = 4 Подставляем значение из промежутка для проверки вместо x, например 2: -2*2²+10*2-8 = -8+20-8 = 4 (+) ,а нас интересуют отрицательные значения Подставляем значение до 1, например -1: -2*(-1²)+10*(-1)-8=-2-10-8=-20 (-) Подставляем значение после 4, например 5: -2*5²+10*5-8=-50+50-8 = -8 (-)
Следовательно, нас устраивают значения от минус бесконечности до 1 (включительно) и от 4 (включительно) до плюс бесконечности.
ответ: 44
Объяснение:
Пусть х — количество учеников, которые были в комнатах по 4 человека. Тогда х/4 — количество четырёхместных комнат (х учеников расселили в комнаты по 4 человека). Количество человек, живших в трёхместных комнатах — 71-х (т. к. все, кто не жил в четырёхместных комнатах, жили в трёхместных). Тогда количество трёхместных комнат — (71-х)/3 (71-х человек расселили в комнаты по трое). Так как всего комнат 20, и они были только трёхместные и четырёхместные, получаем:
20=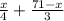
(20 комнат — это все комнаты, и трёхместные, и четырёхместные).
Решим получившееся уравнение:
20=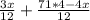
20 =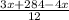
20=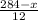
Умножим обе части на 12:
240 = 284 - х
х = 284 - 240
х = 44
ответ: 44.
Примечание: чтобы убедиться в правильности ответа, можно сделать проверку:
Если в комнатах по 4 человека жили 44 ученика, всего четырёхместных комнат было 44/4=11.
Т. к. всего комнат 20, то трёхместрых комнат 20-11=9 комнат. Т. к. все они заполнены, в них должно жить 9*3=27 учеников.
После того, как 44 ученика поселили в четырёхместные комнаты, осталось 71-44=27 детей — именно столько должно было жить в трёхместных комнатах.
Проверка показала, что найденный ответ верен.