Объяснение:
см фото
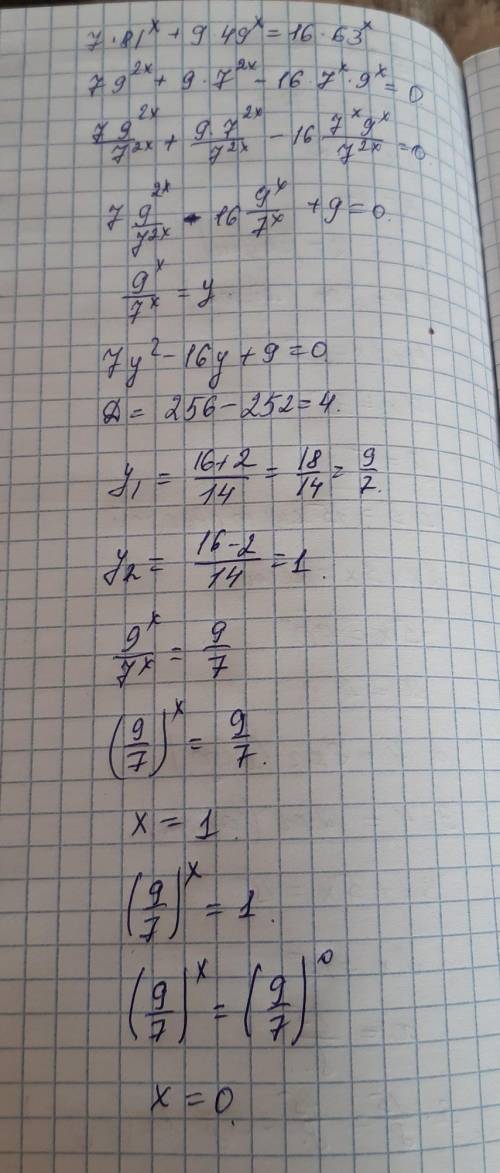
2) f(x) =x / 16 + x^2
У дроби знаменатель не должен никогда равнятся нулю, так как на ноль делить нельзя, поэтому
16+х^2 не равно 0
х^2 не равно 16
х не равен +-4
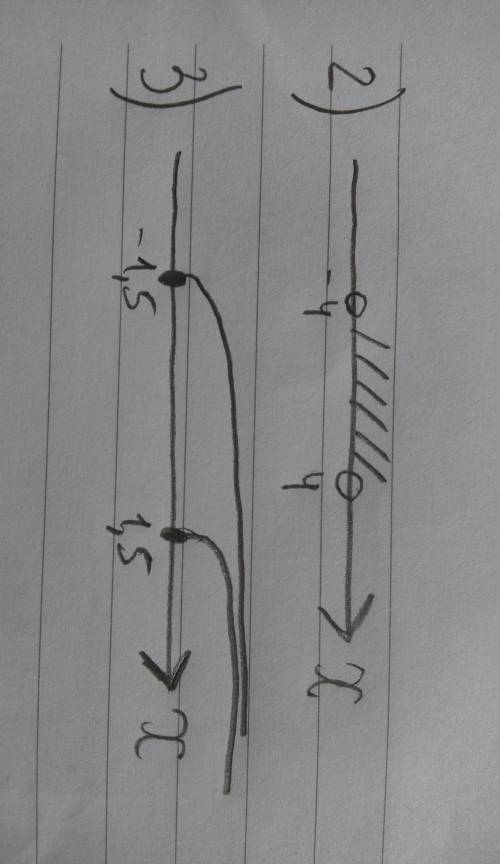
Тут надо нарисовать ось Х(забыла как называется), на ней отметить точки 4 и -4 и записать полученный интервал(будет на фото)
D(y)=(-4;4)-это ответ
3)f(x) =корень из х^2 – 2,25
Здесь работает другое правило:подкоренное выражение всегда больше или равно нулю.
х^2-2,25 больше или равно 0
х^2 больше или равно 2,25
х больше или равно +-1,5
Здесь тоже надо нарисовать ось Х, отметить полученные точки и написать ответ(будет на фото)
D(y) =(1,5;+бесконечности)
Объяснение:
7 * (9)^2x + 9 * (7)^2x = 16 * (7)^x * (9)^x
делим на (7)^x * (9)^x
7 * (9/7)^x + 9 * (7/9)^x = 16
(9/7)^x = t
7 * t + 9 /t = 16
умножим на t
7 * t ² - 16t + 9 = 0
d=256-4*7*9=4
t₁=(16-2)/14=1=(9/7)^x₁ => x₁=0
t₂=(16+2)/14=9/7=(9/7)^x₂ => x₂=1
ответ х ∈ { 0; 1 }