Математика: Кто основал город лондон и в каком году? (ответ короткий )

Кто основал город лондон и в каком году? (ответ короткий )

👇

Увидеть ответ

Ответ:

veronika13571

07.01.2021

Лондон был основан в 43 году н. э. во время вторжения в Британию римлян во главе с императором Клавдием.

4,7(69 оценок)

Ответ:

OniksX

07.01.2021

В I веке до нашей эры на месте кельтского поселения римляне создали город, названный Лондиниум. В 884 году Альфред Великий сделал Лондон столицей своего государства, с 976 года - времени англосаксонского господства - город становится местом пребывания королевской власти.

4,6(21 оценок)

Открыть все ответы

Ответ:

ЛилияЕршова

07.01.2021

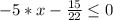
$-5*x-\frac{15}{22} \leq 0\\$

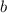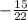По условии видим, что надо решить неравенство с коэффициентом при переменной , которое равняется - 5, с коэффициентом , которому соответствует дробь $-\frac{15}{22}$ .

Решать неравенство необходимо, следуя алгоритму, то есть: перенести дробь 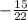$-\frac{15}{22}$ в другую часть с противоположным знаком, разделить обе части на - 5, изменить знак неравенства:

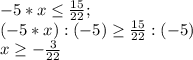
$-5*x\leq \frac{15}{22} ;\\(-5*x):(-5)\geq \frac{15}{22} :(-5)\\x\geq -\frac{3}{22}$

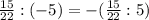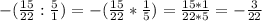При последнем переходе для правой части используется правило деления числе с разными знаками $\frac{15}{22} :(-5)=-(\frac{15}{22} :5)$ ,после чего выполняем деление обыкновенной дроби на натуральное число $-(\frac{15}{22} :\frac{5}{1} )=-(\frac{15}{22} *\frac{1}{5} )=\frac{15*1}{22*5} =-\frac{3}{22}$ .

ответ: и ∞.

Пошаговое объяснение:

4,6(96 оценок)

Ответ:

kononovadm

07.01.2021

1) b-a<-2 ⇔ a>b+2

Знак ''<'' сменился на ''>'', а это означает что все числа/буквы при перестановке поменяют свой знак. Был - , стал +. Был + , стал -

В нашем случае ''b'' не сменит знак (''b'' как стояло в части где знак указывает меньше так и осталось стоять)

''-a'' сменит знак(сначала ''-а'' стояло в части где знак указывает меньше, потом оно стоит в части где знак указывает больше(знак должен сменится))

''-2'' также сменит свой знак(сначала ''-2'' стоит в части где знак указывает больше, потом оно стоит в части где знак указывает меньше(знак должен сменится))

2) a-b>-1 ⇔ a>b-1

Знак не сменился, но некоторые компоненты переставили.

''а'' не сменит знак(''а'' как стояло в части где знак указывает больше так и осталось стоять)

''-b''сменит знак(сначала ''-b'' стояло в части где знак указывает больше, потом оно стоит в части где знак указывает меньше(знак должен сменится))

''-1'' не сменит знак(''-1'' как стояло в части где знак указывает меньше так и осталось стоять)

Надеюсь понятно)

4,5(5 оценок)

Это интересно:

Взаимоотношения

03.09.2021

Как встречаться с юристом: советы и рекомендации...

Кулинария-и-гостеприимство