Объяснение:
a)
x²=xy+3
xy=-2 подставим это в первое уравнение
x²=-2+3=1
x₁=1 y₁=-2/x=-2
x₂=-1 y₂=-2/(-1)=2
b)
x(y+1)=0
x+5xy+y=4
1й случай х=0 подставим во второе уравнение получим у=4
2й случай у+1=0 у=-1 подставим во второе уравнение получим
х-5х-1=4 ; -4x=5 x=-5/4=0,8
c) этот пример не видно
другой номер
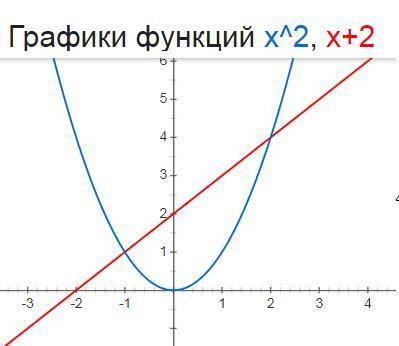
a) y=x^2 это парабола с вершиной в точке (0;0)
y=x+2 это прямая у=х которая является биссектрисой первой координатной четверти перемещенная вверх на 2 единицы
построим схематично графики
видно что графики имеют две точки пересечения значит система имеет два решения
если решать этот пример через дискриминант то тогда
x²=x+2
x²-x-2=0
d=1+8=9
x₁₋₂=(1±3)/2={-1;2}
На первую позицию можно ставить одну из десяти букв, на вторую, одну из девяти и т.д. Получим: 10!
Найдём количество которыми можно составить слово математика из данного набора букв при учёте позиции той или иной буквы.
Е, И и К могут занимать только одну позицию, а вот А, М и Т можно менять местами.
Для М и Т это будет 2! и 2!, для А – 3!
С учётом порядка позиции их будет:
Тогда вероятность (согласно классическому определению):
Попробуем другой, более простой
Перестановки с повторением.
Всего у нас
Перестановка с повторением, которая даёт нам слово "Математика" всего одна, потому мы получаем вероятность: