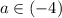
Объяснение:
Проверим случай p=5, уйдет квадратичная часть, но линейная останется, значит неравенство не будет выполняться для всех x.
При p не равном 5 график левой части неравенства представляет собой параболу, для того, чтобы неравенство было верно для любого x вся парабола должна лежать ниже оси абсцисс, т. е. ветви вниз(p-5<0) и D(дискриминант)<0.
D1=(2p-4)^2-4(p-5)(-p-3)=8p^2-24p-44<0
2p^2-6p-11<0
D2=36+88=124
p1=(3-sqrt(31))/2
p2=(3+sqrt(31))/2
D1<0 при
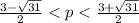
Эти значения p меньше пяти(т.е. ветви направлены вниз). Заносим их в ответ.
каждую скобку приравниваем к нулю и находим корни:
y-5=0
y=5
y+11=0
y=-11
Или решаем по дискриминанту(но будет дольше):
y^2+11y-5y-55=0
y^2+6y-55=0
D=b^2-4ac=36+4*1*55=256
y1=(-6+16)/2=5
y2=(-6-16)/2=-11
2)t^2+12t=0
t(t+12)=0
t1=0
t2=-12
3)-x^2+25=0
x^2-25=0
(x-5)(x+5)=0
x1=5
x2=-5