предыдущее решение не правильно, т.к теплоход не все время плыл по течению, он три раза плыл по течению (х+2)км/ч, и два раза против течения (х-2)км/ч.
Теплоход совершил три хода по течению со скоростью x+2 и два хода против течения соответственно со скоростью x-2. Теперь, время было затрачено одно, следовательно, мы имеем полное право приравнять два выражения, а именно: (S / 2) = (3*S)/(x+2) + (2*S)/(x-2). Приводим к общему знаменателю 2(х+2)(х-2), таким образом получилось следующее: 6Sx(x-2)+4S(x+2)=S(x+2)(x-2)
6Sx-12S+4Sx+8S=Sx^2-4
10Sx-4S=Sx^2-4S (-4S) сокращаем с обоих сторон
10x^2-10Sx=0 x выносим за скобки
x(Sx-10S)=0 следовательно если равно 0, то одна из этих частей равно 0, т.е.
x1=0 или Sx-10S=0
Sx=10S
x= 10S / S
x2=10 км/ч
х1 не удовлетворяет решению задачи, а вот х2 подходит.
Так же не стоит забывать про ОДЗ
ОДЗ:
х+2 не равно 0 след. х не равно -2
х-2 не равно 0 след. х не равно 2
ОДЗ не мешаю решению задачи в данном случае.
ответ: Собственная скорость теплохода равна 10 км/ч
P.S. x^2 -это х в степени 2, если кто не знает)))
x = -π/4 + π*N, N∈Z
tg x=-5/6
x = arctg (-5/6)+ π*N, N∈Z
Объяснение:
3sin²x + 11sinxcosx + 2cos²x = -3
3sin²x + 11sinxcosx + 2cos²x + 3 = 0
Применим основное тригонометрическое тождество sin²x + cos²x = 1
3sin²x + 11sinxcosx + 2cos²x + 3(sin²x + cos²x) = 0
6sin²x + 11sinxcosx + 5cos²x = 0
Разделим обе части уравнения на cos²x
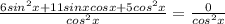
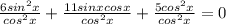
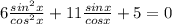
6tg²x + 11 tgx + 5 = 0
Заменим переменную y = tgx
6y² + 11y + 5 = 0
D = 11² - 4*6*5 = 121 - 120 =1
y₁ = (-11 - 1)/12 = -1; y₁ = (-11 + 1)/12 = -10/12 = -5/6
Находим значение переменной х
tgx = -1
x = -π/4 + π*N, N∈Z
tg x=-5/6
x = arctg (-5/6)+ π*N, N∈Z
1) 3х - х = -8 + 4
2х = -4
х = -4 : 2
х= -2
ОТВЕТ: -2
2) 5х - 15 = 2х + 15
5х - 2х = 15 +15
3х = 30
х = 30:3
х = 10
ОТВЕТ: 10