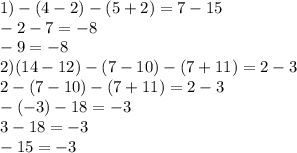
1) Квадратным уравнением называют уравнение ax^2+bx+c=0, где x — переменная, a, b и c — действительные числа, причем a не равно 0.
При этом a называют старшим или первым коэффициентом, b — вторым коэффициентом, c — свободным членом.
2) полные
неполные
приведённые
3) Корни квадратного уравнения ax^2+bx+c=0 находятся по формуле:
x=-b±√D/2a, где D^2-4ac - дискриминант квадратного уравнения
4)Если дискриминант больше нуля, то квадратное уравнение имеет два различных действительных корня.
Если дискриминант равен нулю, то квадратное уравнение имеет только один действительный корень, или, что то же самое - два равных действительных корня, которые равны.
5) Приведённое квадратное уравнение - это квадратное уравнение, у которого первый коэффициент равен 1.
Квадратное уравнение вида x^2+px+q=0 называется приведённым.
Квадратное уравнение называют приведённым, если его коэффициент равен 1
Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру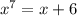 
уравнение в действительных корнях.
Рассмотрим функцию 
. Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию 
. Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение 
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.
