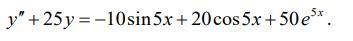
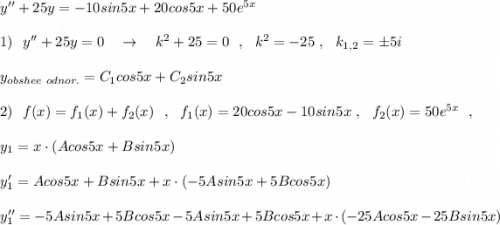
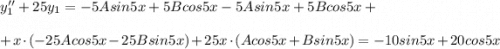
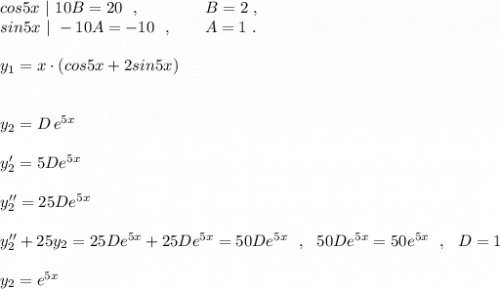
Объяснение:
sin1845° можно представить как sin(1800°+45°)
Так как π=180°, то 1800°=10π, то есть sin(1800°+45°)=sin(10π+45°)
Дальше есть несколько путей нахождения необходимого значения. Во-первых, период синуса - 2π, то есть sin(2π+x)=sin(x), тогда sin(10π+45°)=sin(45°)=√2/2
Во-вторых, можно раскрыть по формуле синуса суммы:
sin(a+b)=sin(a)cos(b)+cos(a)sin(b)
sin(10π+45°)=sin(10π)cos(45°)+cos(10π)sin(45°)=0*√2/2+1*√2/2=√2/2
В-третьих, можно узнать значение функции с формул приведения. Так как аргумент отсчитывается от горизонтальной оси, смены функции на кофункцию (косинус) не будет; изначальная функция положительна (I четверть на тригонометрической окружности), поэтому знак будет тоже "+".
Объя1) (х+у)(х-у)=х²-ху+ху-у²=х²+(-ху+ху)-у²=х²-у²
2) (Р+Т)(Р-Т)=Р²-РТ+РТ-Т²=Р²+(-РТ+РТ)-Т²=Р²-Т²
3)(m+5)(m-5)=m²-5m+5m-25=m²+(-5m+5m)-25=m²-25
4)(n+1)(n-1)=n²-n+n-1=n²+(-n+n)-1=n²-1
5)(5a-b)(5a+b)=25a²+5ab-5ab-b²=25a²+(5ab-5ab)-b²=25a²-b²
6)(2m+3)(2m-3)=4m²-6m+6m-9=4m²+(-6m+6m)-9=4m²-9
7)(2a-3b)(3b+2a)=6ab+4a²-9b²-6ab=(6ab-6ab)+4a²-9b²=4a²-9b²
8)(7m+3n)(7m-3n)=49m²-21mn+21mn-9n²=49m²+(-21mn+21mn)-9n²=49m²-9n²
9)(7m+3n)(7m-3n)=49m²-21mn+21mn-9n²=49m²+(-21mn+21mn)-9n²=49m²-9n²
объясняю первое остальное по аналогии делается
в принципе существует формула сокращённого умножения, но она относится к тем примерам в скобках которых находятся подобные члены, но с противоположными знаками
(х+у)(х-у)=
раскрываем скобки перемножив все члены
х·х-х·у+х·у-у·у=
х²-ху+ху-у²=
группируем
х²+(-ху+ху)-у²=х²-у²снение:
попрубуй повторить как у меня ок?