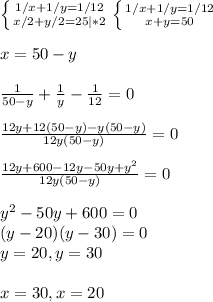
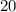 ч., 2 рабочий - за
ч., 2 рабочий - за 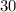 ч.
ч.
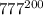 ≡
≡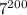 (mod 10). Найдем несколько степеней числа 7:
(mod 10). Найдем несколько степеней числа 7: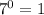
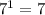
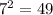
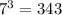
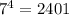
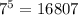
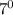 и
и 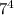 оканчиваются на одну цифру 1;
оканчиваются на одну цифру 1; 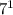 и
и 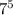 также оканчиваются на одну цифру 7. Последняя цифра в степенях числа 7 будет повторяться через 4, т.е., более строго, для любых целых неотрицательных чисел m и n верно утверждение:
также оканчиваются на одну цифру 7. Последняя цифра в степенях числа 7 будет повторяться через 4, т.е., более строго, для любых целых неотрицательных чисел m и n верно утверждение: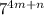 ≡
≡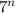 (mod 10)
(mod 10)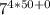 ≡
≡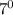 (mod 10)
(mod 10)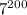 ≡
≡ (mod 10)
(mod 10)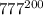 ≡
≡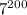 (mod 10), то
(mod 10), то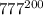 ≡
≡ (mod 10).
(mod 10).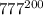 равна 1.
равна 1.