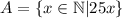
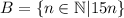
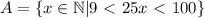
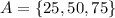
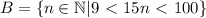
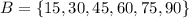
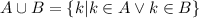- то есть, это такое множество всех k, так что, либо k в А либо в В, или в А и в В одновременно.
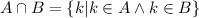- то есть, это такое множество всех k, так что, k и в А и в В одновременно.
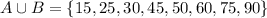- то есть, это множество всех чисел которые кратны либо 25 либо 15, или 25 и 15 одновременно.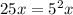
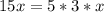
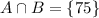
а²-4а+5
Дробь равна нулю тогда и только тогда, когда числитель равен 0, а знаменатель не равен 0:
а³-25а=0,
а²-4а+5≠0
решаем уравнение: а³-25а=0, а(а²-25)=0 , произведение множителе равно нулю тогда и только тогда , когда хотя бы один из множителей равен 0:
а=0 или а²-25=0
а²=25, а=5, а=-5
Проверка:
найденные значения подставляем во второе условие.
а=0, 0²-4·0+5=5≠0-явл. корнем
а=5, 5²-4·5+5=25-20+5=10≠0-явл. корнем
а=-5, (-5)²-4·(-5)+5=25+20+5=50≠0-явл. корнем
ответ:дробь равна 0 при а=0,а=5,а=-5