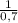Пусть 
(км/ч) - первоначальная скорость мотоциклиста.
Тогда время, за которое он преодолел путь в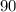 
километров, равно 
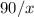часов.
Но, с другой стороны, сумма трех других отрезков времени равна тому же промежутку времени (по условию). Это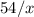 
часов, 
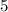минут или же 
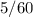часа = 
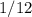часа. И последний промежуток, 
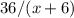часов (
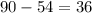километров со скоростью 
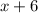км/ч).
Теперь, конечно, будем решать уравнение:
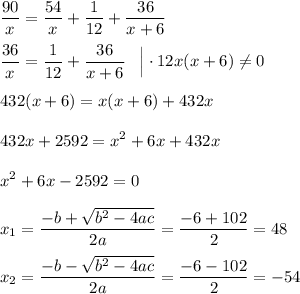
Получилось два корня. Второй доверия не внушает из-за своей отрицательности, так что возьмем исключительно первый.
Первоначальная скорость мотоциклиста -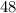 
км/ч.
Задача решена!
ответ: 48 км / ч .
1. Найдите производные функций
А) y= x6 y`=6x5
б) y = 2 y`=0
в) y=5/x y`=-5/x^2
г) y = 3-5x y=-5
д) y= 8 √x + 0,5 cos x y`=4/Vx -0.5sinx
е) y=sinx / x y`={xcosx-sinx}/x^2
ж) y= x ctg x y`={ctgx-x/sin^2x}=cosx/sinx- x/sin^2x={cosxsinx-x}/sin^2x
з) y= (5x + 1)^7 y`=5*7(5x+1)^6=35(5x+1)^6
2.Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции:
y= x^8/8 – x^5/5 - x √3 – 3 в точке x0= 1
y`=x^7-x^4-V3 tga=y`(1)=1-1-V3=-V3 a=120*
3. Вычислите если f(x)=2cos x+ x2- +5 что надо?
4. Прямолинейное движение точки описывается законом s=t4 – t2(м). Найдите ее скорость в момент времени t=3с.
v=s`=4t3-2t
v(3)=4*27-2*3=108-6=102 м/с
5. Найдите все значения х, при которых выполняется неравенство f/(x)<0, если
f(x)= 81x – 3x3
f`=81-9x^2=9(3-x)(3+x)
-3 3
- + -
xe(-oo,-3)U(3,+oo)
6. Найдите все значения х, при которых выполняется равенство f/(x)=0, если f(x)=cos2x - x√3 и x€[0,4π].
ответ: -2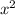
+7х=0
х(-2х+7)=0
х=0, -2х+7=0
-2х=-7
х=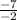
ответ : 0,-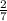
-2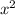
-х=0
х(-2х-1)=0
х=0, -2х=1
х= -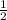
ответ:0,-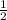
-0.7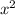
+х=0
х(0.7х+1)=0
х=0, 0,7х=-1
х=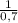
ответ: 0,