
32 см
Объяснение:
Пусть х см - ширина прямоугольника, тогда
(х+4) см - длина прямоугольника
(х(х+4)) кв.см -площадь прямоугольника
Т.к. по условиям задачи площадь равна 60 кв.см , составим и решим уравнение.
х(х+4)=60
х^2+4х=60
х^2+4х-60=0
а=1 b=4 c=-60
D=b^2-4ac=4^2-4*1*(-60)=16+240=256
x=(-b+корень D)/2а=(-4+корень 256)/2*1=(-4+16)/2=12/2=6
x=(-b-корень D)/2а=(-4-корень 256)/2*1=(-4-16)/2=-20/2=-10
-10 - значения стороны не может быть отрицательным
6 см-ширина прямоугольника
1) Находим периметр периметр по формуле 2*(a+b)=2*(6+(6+4))=32 см
n^2 - это число во второй степени
ответ:1.а Раскрываем скобки.25-10х+х2 - 4-4х-х2. х2 и - х2 взаимно уничтожаются и остается -14х+21.Здесь мы может вынести за скобки общий множитель(-7). ответ:-7(2х-3).
б 3а2+4а+2-а2=2а2+4а+2.Выносим общий множитель за скобки (2). 2(а2+2а+1).Видим формулу квадрата суммы.Можно поменять.ответ:2(а+1)^2
в х2-у2 - (х-у).Видим формулу разности квадратов и знаем чему она равна и подставляем.Получаем (х-у)*(х+у)-(х-у).Здесь у нас повторяется х-у ,поэтому оно будет общим. Получаем (х-у)*(х+у-1).
3 а2+2аб+б2-с2.Видим формулу квадрата суммы. Подставляем.(а+б)^2 - с2. Все у нас в квадрате поэтому будет 2 скобки ( в первой все знаки не меняем а во второй меняем знак после скобки на противоположный)Получаем (а+б-с)*(а+б+с).
б2+а2-2аб-х2.Тоже видим формулу квадрата разности.Подставляем .(а-б)^2 -х2.Получаем (а-б-х)*(а-б+х).
Со вторым заданием разберешься сама там не сложно и все по формулам.
Задание №1
а).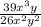 (сокращаем на "13
(сокращаем на "13 y")
y")
ответ: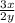
б).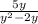 (в знаменателе выносим "y" и сокращаем с "y" в числителе)
(в знаменателе выносим "y" и сокращаем с "y" в числителе)
ответ: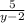
в).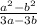 (раскрываем числитель по формуле разности квадратов
(раскрываем числитель по формуле разности квадратов 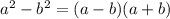 , в знаменателе выносим "3")
, в знаменателе выносим "3")
ответ: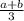
Задание №2
а).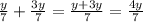 (одинаковый знаменатель, значит можно складывать)
(одинаковый знаменатель, значит можно складывать)
ответ: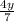
б).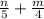 (знаменатели разные, чтобы сложить приводим к общему знаменателю. Первую дробь умножаем на 4, вторую умножаем на 5, после чего складываем)
(знаменатели разные, чтобы сложить приводим к общему знаменателю. Первую дробь умножаем на 4, вторую умножаем на 5, после чего складываем)
ответ: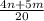
в). (принцип тот же. "а" есть и там, и там в знаменателе, значит первую дробь умножаем на 3, вторую умножаем на 2, чтобы получить общий знаменатель, после чего вычитаем)
(принцип тот же. "а" есть и там, и там в знаменателе, значит первую дробь умножаем на 3, вторую умножаем на 2, чтобы получить общий знаменатель, после чего вычитаем)
ответ: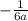
г).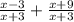 (знаменатель одинаковый - складываем)
(знаменатель одинаковый - складываем)
ответ: 2
Задание №3
а).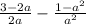 (умножаем первую дробь на a, а вторую умножаем на 2, после чего вычитаем дроби)
(умножаем первую дробь на a, а вторую умножаем на 2, после чего вычитаем дроби)
ответ: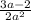
б). (первую дробь умножаем на знаменатель второй дроби, а вторую дробь умножаем на знаменатель первой дроби, после чего вычитаем)
(первую дробь умножаем на знаменатель второй дроби, а вторую дробь умножаем на знаменатель первой дроби, после чего вычитаем)
ответ: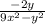
в).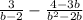 (вынесем "b" в знаменателе второй дроби за скобку и умножим первую дробь на "b", после чего вычитаем)
(вынесем "b" в знаменателе второй дроби за скобку и умножим первую дробь на "b", после чего вычитаем)
ответ: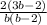
Задание №4
ответ: -40
Задание №5
Первую дробь умножим на "х" и на "x+4", среднюю дробь умножим на "х", а третью дробь умножим на "x+4" и на "x-4", после чего посчитаем)