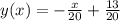1) cos 2x - 5cos x - 2 = 0
2 cos²x - 1 -5cos x - 2 = 0
2 cos²x -5cos x - 3 = 0
Нехай cos x= t
2 t² -5t- 3 = 0
D=25+24=49
t1=(5+7)/4=3 - не задовольняє умову
t2=(4-7)/4=-1/2
cos x=-1/2
x= ±2π/ 3 +2 πn, n ∈ Z
2) 2 sin²x =√ 3 * sin 2x
2 sin²x -2√ 3 sin xcos x=0
2 sinx( sinx-√ 3cos x)=0
2sinx=0
x=πn, n ∈ Z
sinx-√ 3cos x=0
1/2sinx-√ 3/2cos x=0
sinπ/6sinx-cosπ/6cos x=0
-sin(π/6-x)=0
sin(x-π/6)=0
x-π/6=πn
x=π/6 + πn, n ∈ Z
3) 5 cos 2x + 2 sin 2x = 0
5 + 2 tg 2x=0
tg 2x=5/2
2x=arctg5/2 + πn
x=arctg5/4 + πn/2, n ∈ Z

Уравнение касательной к графику функции в точке имеет вид:
1. Вычисляем значение функции в точке :
н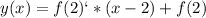
2. Вычисляем производную функции :
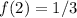
3. Вычисляем значение производной в точке :
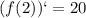
Таким образом, уравнение касательной имеет вид:
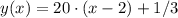
Немного упрощая, получаем:
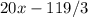
ответ:
Уравнение касательной к графику функции в точке имеет вид:
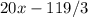
Уравнение нормали к графику функции в точке имеет вид:
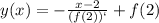
1. Вычисляем значение функции в точке :
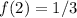
2. Вычисляем производную функции :
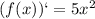
3. Вычисляем значение производной в точке :
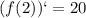
Таким образом, уравнение нормали имеет вид:
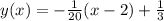
Немного упрощая, получаем:
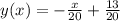
ответ:
Уравнение нормали к графику функции в точке имеет вид: