
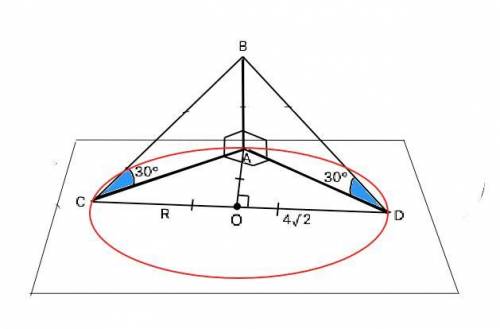
ответ: 8/√3 (ед.длины)
Объяснение: АВ перпендикулярно плоскости альфа ⇒АВ перпендикулярно любой прямой, лежащей в этой плоскости ⇒ АВ⊥АС и АВ⊥АD.
Треугольники АВС и ∆АВD имеют по равному острому углу (дано) и общему катету АВ, следовательно, они равны. из чего следует равенство катетов прямоугольного ∆ АСD, т.е. АС=АD и углы АСD=ADC=(180°-90°):2=45°.
Центром окружности, описанной около прямоугольного треугольника, является середина его гипотенузы. R=CO=DO=4√2. ⇒ медиана АО=R=4√2, а
АС=СО/sin45°=4√2)/√3/2=8 (ед. длины)
Из прямоугольного ∆ АВС катет АВ=АС•tg30°=8•1/√3=8/√3
Коэффициент = 714
Объяснение:
-4,2с³b ²a * (-2 3/7)a⁴dc=
(-42/10)*(-17/7)*a*a⁴*b²*c³*c*d=
(294*170/70)*a⁵*b²*c⁴*d=
714a⁵b²c⁴d - стандартный вид
коэффициент = 714