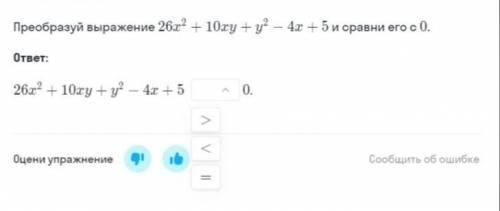
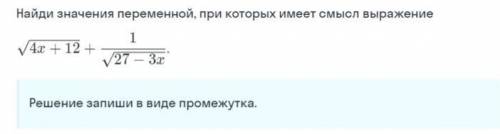
Пусть СЕ =х , тогда ВЕ= 32-х, АД= 16-х ВД= 24-(16-х) = 8+х. Треугольники ВДЕ и АВС подобны по двум углам ( угол в -общий , угол ВЕД= углу С как соответственные при параллельных ДЕ И АС и секущей ВС) Значит ВД/ ВА = ВЕ/ВС тоесть (8+х) : 24= (32-х) :4 , решаем эту пропорцию (8+х)* 32= (32-х)* 24
( 8+х)* 4= (32-х)* 3
32 +4х= 96 -3х
7х=64
х= 9 целых 1/7
ВД= 8+9 целых 1/7= 17 целых 1/7
Также пропорциональны стороны ВД : АВ= ДЕ : АС подстави данные 17 целых 1/7 : 24= ДЕ : 28, ДЕ = 17 целых 1/7 * 28 :24 = 20 см
ответ 20см
Где
1)
Поначалу у функции
Это степенная функция, а производная любой степенной функции находится следующей формулой:
В нашем случае:
Так, нашли производную общего случая.
Так как, точки касания не даны, мы запишем нахождение касательной в любой точке этой функции:
2)
Опять же, найдем производную
Так как, точки касания не даны, мы запишем нахождение касательной в любой точке этой функции:
То есть, берешь любой икс, и вставляешь в выражение касательной вместо
Это и есть окончательные ответы.
Если что-то не правильно, то это значит что вы не правильно написали условие.