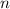 месяцев взяли
месяцев взяли 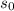 рублей. Тогда:
рублей. Тогда: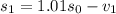
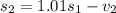
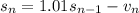 ,
,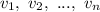 - выплаты в 1, 2, ..., n месяце. Заметим, что последний остаток
- выплаты в 1, 2, ..., n месяце. Заметим, что последний остаток 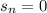 , так как через n месяцев весь кредит выплачен.
, так как через n месяцев весь кредит выплачен.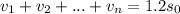
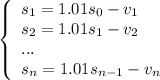 сложим все уравнения, после чего слагаемые вида
сложим все уравнения, после чего слагаемые вида 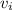 перенесем влево, а слагаемые вида
перенесем влево, а слагаемые вида 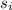 - вправо.
- вправо.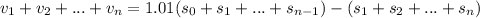
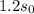 :
: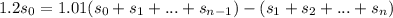
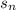 :
: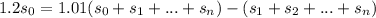
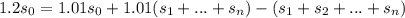
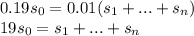
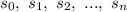 уменьшаются равномерно, то есть составляют арифметическую прогрессию.
уменьшаются равномерно, то есть составляют арифметическую прогрессию. :
: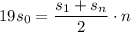
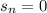 , то выражение упрощается:
, то выражение упрощается: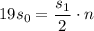
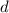 . Тогда:
. Тогда: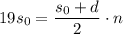
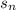 через первый член и разность прогрессии:
через первый член и разность прогрессии: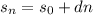
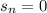 , то
, то 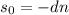 . Подставляем в соотношение:
. Подставляем в соотношение: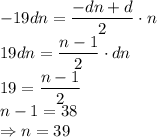
Смотри решение на фото ниже