Объяснение:
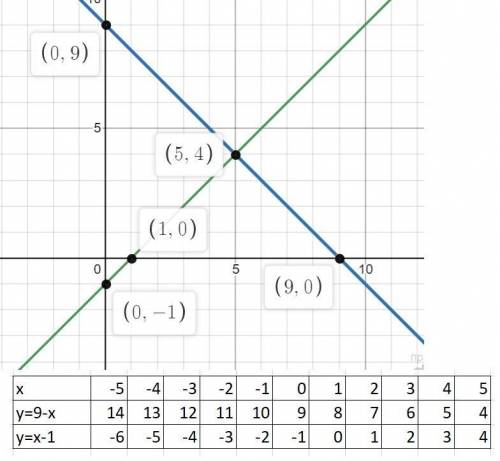
1) x+y=9; y=9-x;
x-y=1. y=x-1;
Составляем таблицу значений изменения функций при изменении аргумента и строем графики. Точка пересечения и является решением: (5;4)
(См. скриншот)
-------------
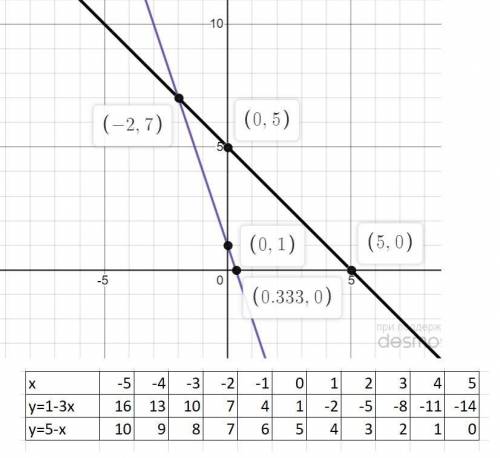
2) 3x+y=1; y=1-3x
x+y=5; y=5-x.
Составляем таблицу значений изменения функций при изменении аргумента и строем графики. Точка пересечения и является решением: (-2;7)
(См. скриншот)
---------------------
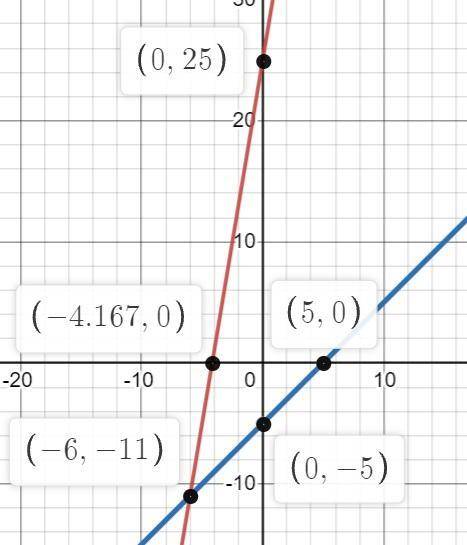
3) y-6x=-25; y=25+6x;
y-x=-5; y=x-5;
Составляем таблицу значений изменения функций при изменении аргумента и строем графики. Точка пересечения и является решением: (-6;-11)
(См. скриншот)
------------------------
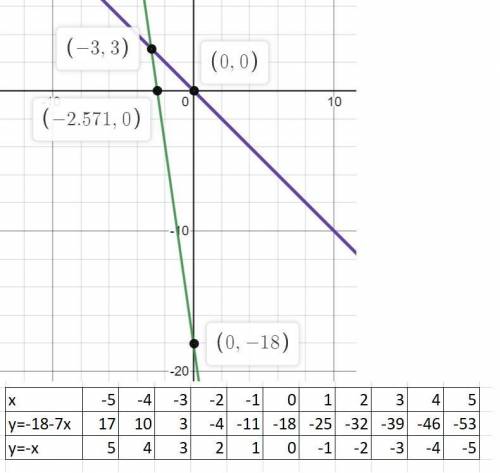
4) y+7x=-18; y=-18-7x;
y+x=0; y=-x;
Составляем таблицу значений изменения функций при изменении аргумента и строем графики. Точка пересечения и является решением: (-3;3)
(См. скриншот)
Числитель первой дроби разложим на множители по формуле разности квадратов двух выражений a² - b² = (a - b)(a + b), где a = a, b = 3b. В знаменателе второй дроби вынесем за скобку общий множитель 4.
((a - 3b)(a + 3b))/4a² * a/(4(a + 3b).
Сократим а² и а на а. Сократим (а + 3b) и (a + 3b).
(a - 3b)/4a * 1/4 = (a - 3b)/(4a * 4) = (a - 3b)/16a = a/16a - 3b/16a = 1/16 - 3b/16a.
a = √2, b = √18; 1/16 - (3√18)/(16√2) = 1/16 - 3/16 * √(18/2) = 1/16 - 3/16 * √9 = 1/16 - 3/16 * 3 = 1/16 - 9/16 = -8/16 = -1/2 = -0,5.
ответ. -0,5.
Удачи✅✊