3. Решите уравнение: 1)|x|=3; 2) |x-3|= 2; 3) |x-4|=0; 4) |x+3|=-4;

Question

Алгебра: 3. Решите уравнение: 1)|x|=3; 2) |x-3|= 2; 3) |x-4|=0; 4) |x+3|=-4;

Кирвалидзе · Accepted Answer

чтобы найти точку минимума (или максимума), нужно найти производную и приравнять к нулю.

наша функция

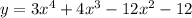
$y = 3 {x}^{4} + 4 {x}^{3} - 12 {x}^{2} - 12$

ее производная

найдем производную:

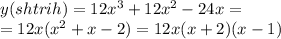
$y(shtrih) = 12 {x}^{3} + 12 {x}^{2} - 24x = \\ = 12x( {x}^{2} + x - 2) = 12x(x + 2)(x - 1)$

отсюда видна, что у'=0 в точках

х1 = 0 ; х2 = 1; х3 = -2

Данный точки являются точками экстремума.

- + - +

--------------|----------------|-----------|---------------->х

-2. 0. 1

min. max. min

найдем значение функции в этих точках

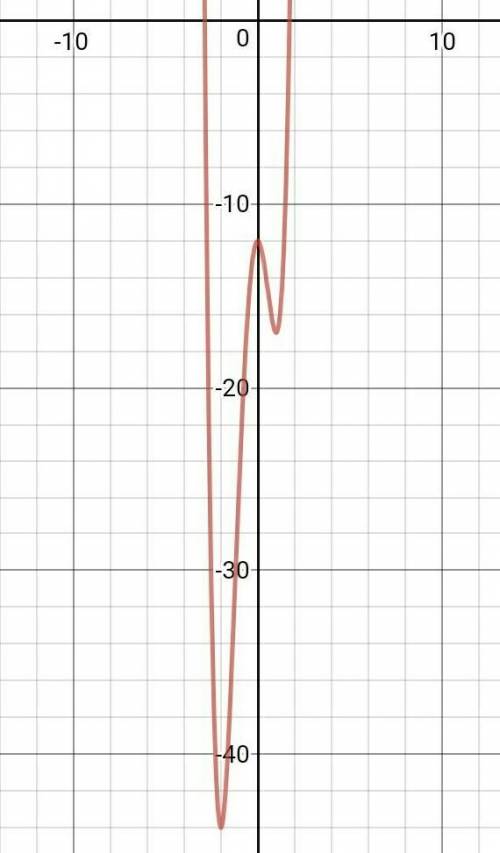
у(0) = -12;. у(1) = -17;. у(-2) = -44

Дополнительно найдем значения на концах отрезка

у(-5) = 1063;. у(1/2)=-14.31

точки локального минимума

(-2; -44)

(1; -17)

минимум достигается в точке (-2; -44)

+наглядный график