Объяснение:
Требуется построить график функции и определите при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
1.
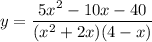
Разложим числитель на множители. В знаменателе вынесем х из первой скобки:
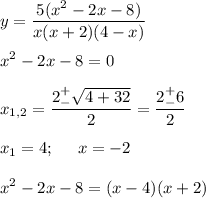
Далее вынесем минус и сократим дробь. Не забываем про область определения функции:
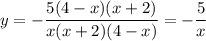
Dy: x ≠ 0; x ≠ -2; x ≠ 4;
или х ∈ (-∞;-2) ∪ (-2;0) ∪ (0;+∞)
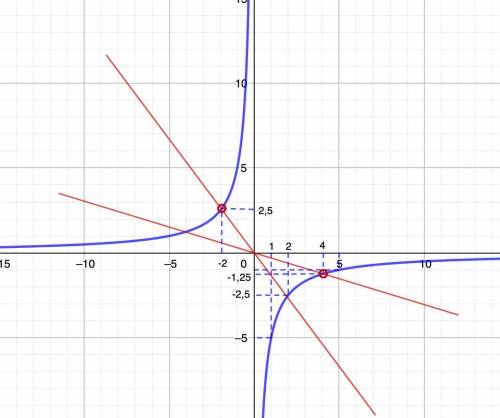
2. Строим график - гипербола, расположена во 2 и 4 четвертях.
Возьмем точки:
х=1; y=-5;
x=2; y=-2,5;
x=5; y=-1
Вторую ветвь гиперболы строим симметрично начала координат.
Отметим "выколотые" точки.
x ≠ -2; x ≠ 4
3. При каких значениях k прямая y=kx имеет одну общую точку?
Прямая проходит через начало координат.
Эти прямые пройдут через "выколотые" точки.
Подставим их координаты в уравнение прямой и найдем k:
1) (-2; 2,5)
2,5=k*(-2)
k = -1,25 ⇒ y = -1,25x
2) (4; -1,25)
-1,25=k*(4)
k = - 0,3125 ⇒ y = -0,3125x
Пусть событие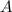 
- "выпало 6 очков", а событие 
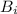- "было произведено i бросков".
Предполагается, что количество бросков определяется случайно, то есть:
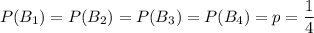
В данном случае конкретное числовое значение не столь важно, главное что оно одинаково для всех гипотез.
Для решения задачи понадобится формула Байеса:
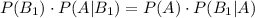
Нам нужно найти вероятность того, что был 1 бросок, при условии того, что выпало 6 очков:
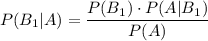
Распишем полную вероятность:
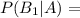
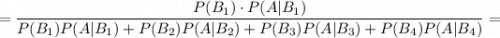
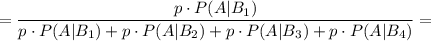
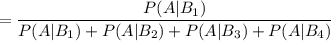
Найдем вероятности выпадения 6 очков при 1, 2, 3, 4 бросках.
При одном броске вероятность выпадения 6 очков, как и любого другого количества очков:
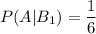
При двух бросках, 6 очков может выпасть в следующих комбинациях:
{1; 5} - 2 вариант
(3; 3) - 1 вариант
{4; 2} - 2 вариант
Благоприятных вариантов - 5. Общее количество вариантов выпадения комбинации на двух кубиках равно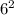 
.
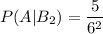
При трех бросках, 6 очков может выпасть в следующих комбинациях:
{1; 1; 4} - 3 варианта
(1; 2; 3) - 6 вариантов
Благоприятных вариантов - 9.Общее количество вариантов выпадения комбинации на трех кубиках равно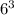 
.
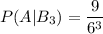
При четырех бросках, 6 очков может выпасть в следующих комбинациях:
{1; 1; 1; 3} - 4 варианта
(1; 1; 2; 2) - 6 вариантов
Благоприятных вариантов - 10.Общее количество вариантов выпадения комбинации на четырех кубиках равно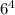 
.
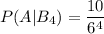
Таким образом, искомая вероятность:
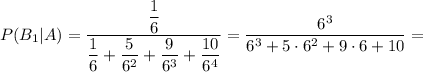
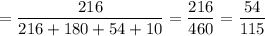
ответ: 54/115
