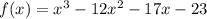
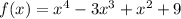
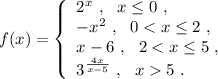
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .
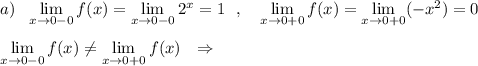
При х=0 функция имеет разрыв 1 рода .
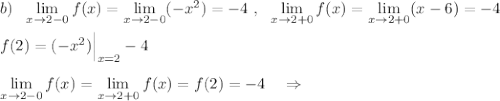
При х=2 функция непрерывна.
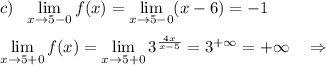
При х=5 функция имеет разрыв 2 рода .
График функции нарисован сплошной линией.
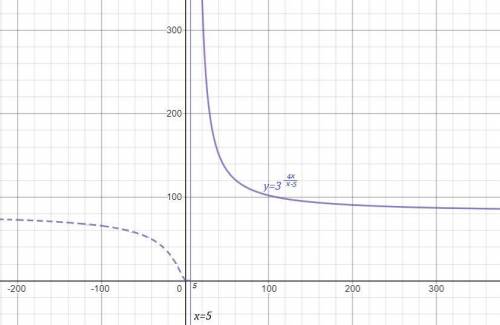
На 1 рисунке нет чертежа функции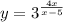 
при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .
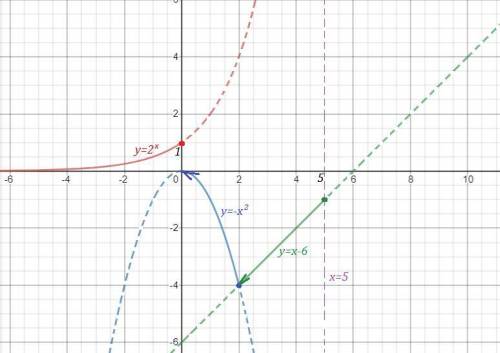
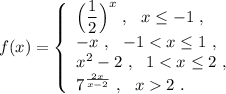
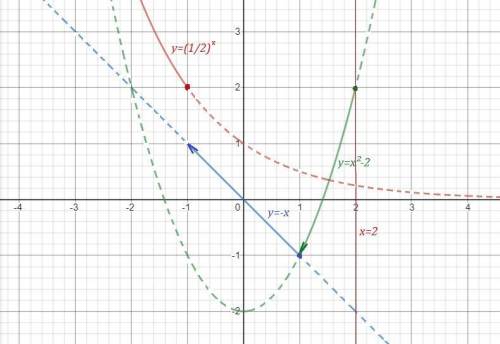
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х= -1, х=1 , х=2 .
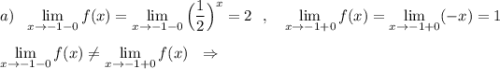
При х= -1 функция имеет разрыв 1 рода .
При х=1 функция непрерывна.
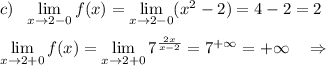
При х=5 функция имеет разрыв 2 рода .
График функции нарисован сплошными линиями.
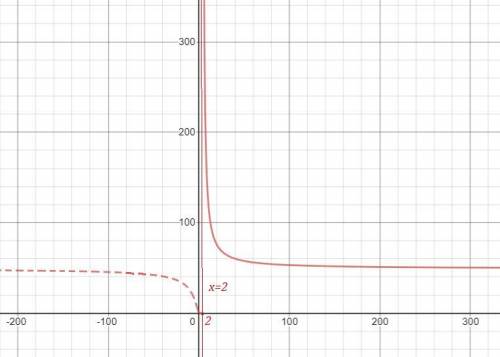
На 1 рисунке нет чертежа функции при х>2 , для которого прямая х=2 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>2 сплошной линией..
Объяснение:
1. Найдите промежутки возрастания и убывания:
Найдем производную, приравняем к нулю, найдем корни.
Определим знаки производной на промежутках. Если "+", функция возрастает, "-" - убывает.
См. рис.
Функция возрастает при х ∈ [-∞; -0,7]∪[8,7; +∞]
или
Функция убывает при х ∈ [-0,7; 8,7]
или
2. Найдите стационарные точки:
Точки области определения функции, при которых производная функции равна нулю, называются стационарными точками.
3. Найдите локальные максимумы и минимумы функции.
Найдем производную, приравняем к нулю, найдем корни.
Определим знаки производной на промежутках. Если производная меняет знак с "+" на "-", то будет точка максимума. Если производная меняет знак с "-" на "+" - точка минимума.
См. рис.