Решение на фото

Решать такое надо графически.
Построим графики уравнений f(x,y)=0 (к 1-му неравенству); g(x,y)=0 (ко 2-му неравенству)
В 1-м неравенстве видно, что это эллипс.
Приведу его к каноническому виду:
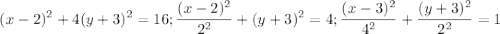
Это значит, что центр эллипса в точке (2;-3), по x он растянется максимум на 4 единицы, по у на 2.
Во 2-м видно, что будут 2 прямые.
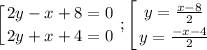
Построили графики на одной системе координат.
1-е неравенство говорит нам, что это геометрическое место точек, которые находятся ВНУТРИ эллипса, причем не захватывая его контур.
Теперь ко 2-му неравенству.
Прямые пересекаются (у них разные угловые коэффициенты) и образуют перекрестие, деля плоскость на 4 части. Нам будут нужны 2 части, это верхняя часть и нижняя, можно это проверить, подставив точку (0;0) во 2-е неравенство и (0;-5).
Получаются два сектора, причем прямые в них включатся в зону, так как 2-е неравенство системы нестрогое, а вот контуры эллипса как бы выколоты. Штриховкой я отметил нужную область.
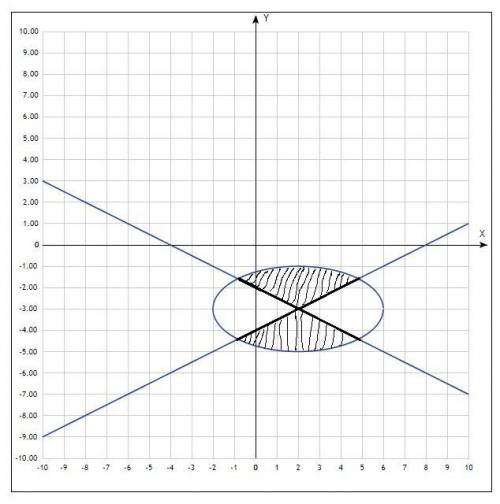
Відповідь:
Пояснення:
1) (2a-3b)(2a+3b) = (2a)²-(3b)²= 4a²-9b²
2)(-y-15b⁵)(y-15b⁵)= -(y+15b⁵)(y-15b⁵)= - (y² - 225b¹⁰)= -y²+225b¹⁰
3) (a-1)(a+1) = a²-1²= a²-1
4) (a⁴-1)(a⁴+1)= (a⁴)²-1²= a¹⁶-1
5) (a²-1)(a²+1) = a⁴-1
6)(a-1)(a+1)(a²+1)(a⁴+1)= (a²-1)(a²+1)(a⁴+1)= (a⁴-1)(a⁴+1)= a¹⁶- 1