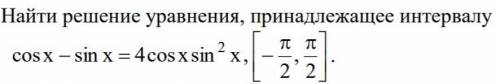

![\displaystyle a)\ \sin\Big(x+\dfrac{\pi }{4}\Big)=0\ \ ,\ \ x+\frac{\pi}{4}=\pi n\ \ ,\ \ x=-\frac{\pi}{4}+\pi n\ ,\ n\in Z\\\\b)\ \ sin\Big(2x-\dfrac{\pi}{4}\Big)=0\ \ ,\ \ 2x-\frac{\pi}{4}=\pi k\ \ ,\ \ 2x=\frac{\pi}{4}+\pi k\ \ ,\ \ x=\frac{\pi}{8}+\frac{\pi k}{2}\ ,\ k\in Z\\\\c)\ \ x\in \Big[-\frac{\pi }{2}\, ;\ \frac{\pi }{2}\ \Big]:\ x=-\frac{3\pi}{8}\ ,\ -\frac{\pi}{4}\ ,\ \frac{\pi }{8}\ .\\\\\\Otvet:\ \ a)\ \ x=-\frac{\pi}{4}+\pi n\ ,\ \ x=\frac{\pi}{8}+\frac{\pi k}{2}\ ,\ \ n,k\in Z\ ;](/tpl/images/2055/8243/a733c.png)
Решение системы уравнений (2; 1)
Объяснение:
Решить методом сложения систему уравнений :
{2х+3у=7
{7х-3у=11
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.
В данной системе ничего преобразовывать не нужно, коэффициенты при у одного значения и с противоположными знаками.
Складываем уравнения:
2х+7х+3у-3у=7+11
9х=18
х=2
Теперь подставляем значение х в любое из двух уравнений системы и вычисляем у:
2х+3у=7
3у=7-2х
3у=7-2*2
3у=7-4
3у=3
у=1
Решение системы уравнений (2; 1)
Объяснение:
((a+7)\(a-7)-(a-7)\(a+7))\(14\(a^2-7a))
Приведем дроби в скобке к общему знаменателю a^2-49, домножив первую дробь на (a+7), а вторую на (a-7):
((a+7)^2-(a-7)^2)\(a^2-49)
По формуле разности квадратов:
((a+7-a+7)(a+7+a-7))\(a^2-49)
14*2a\a^2-49
28a\a^2-49
Представим деление одной дроби на другую умножением первой на перевернутую вторую:
(28a*(a^2-7a))\(14*(a^-49))
Вынесем в числителе "а" за скобку, а в знаменателе разложим скобку на множители:
(28a^2*(a-7))\(14(a-7)(a+7))
Сократим дробь:
2a^2\(x+7)