Турист ехал 5 часов на автомобиле и 8 часов на поезде.он проехал все 1060 км.какова скорость автомобиля,если она на 15км/ч меньше скорости поезда?

👇

Ответ:

ВладАхтубинск

14.02.2023

S=v*t - формула из физики

1060 = 5*Vавто + 8*Vпоезда
1060 = 5*Vавто + 8*(Vавто + 15)
1060 = 5*Vавто + 8*Vавто + 120
940 = 13*Vавто
Vавто = 940/13

4,5(65 оценок)

Ответ:

1660044

14.02.2023

Хкм/ч-скорость автомобиля
х+15км/ч-скорость поезда
5х+8(х+15)=1060
5х+8х=1060-120
13х=940
х=940/13=72 4/13км/ч-скорость автомобиля

4,4(2 оценок)

Открыть все ответы

Ответ:

Aizere1111

14.02.2023

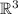Пусть $\varepsilon$ - канонический базис в $\mathbb{R}^{3}$ .

Тогда матрицу перехода 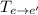$T_{e \rightarrow e'}$ можно найти следующим образом:

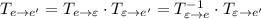
$T_{e \rightarrow e'} = T_{e \rightarrow \varepsilon} \cdot T_{\varepsilon \rightarrow e'} = T_{\varepsilon \rightarrow e}^{-1} \cdot T_{\varepsilon \rightarrow e'}$

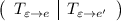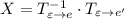
Если записать блочную матрицу $\left(\begin{array}{c|c}T_{\varepsilon \rightarrow e}&T_{\varepsilon \rightarrow e'}\end{array}\right)$ и привести путем элементарных преобразований к виду $\left(\begin{array}{c|c}E&X\end{array}\right)$ , то $X = T_{\varepsilon \rightarrow e}^{-1} \cdot T_{\varepsilon \rightarrow e'}$

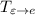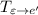Матрицу $T_{\varepsilon \rightarrow e}$ легко получить: достаточно записать в столбцы координаты векторов базиса . Аналогично с матрицей $T_{\varepsilon \rightarrow e'}$ .

В итоге необходимо получить вид $\left(\begin{array}{c|c}E&X\end{array}\right)$ следующей матрицы:

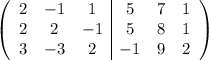
$\left(\begin{array}{ccc|ccc}2&-1&1&5&7&1\\2&2&-1&5&8&1\\3&-3&2&-1&9&2\end{array}\right)$

Вычтем первую строку из второй и третьей:

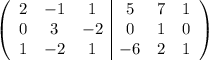
$\left(\begin{array}{ccc|ccc}2&-1&1&5&7&1\\0&3&-2&0&1&0\\1&-2&1&-6&2&1\end{array}\right)$

Вычтем из первой строки 2 третьих и поменяем их местами:

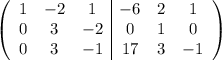
$\left(\begin{array}{ccc|ccc}1&-2&1&-6&2&1\\0&3&-2&0&1&0\\0&3&-1&17&3&-1\end{array}\right)$

Вычтем из третьей строки вторую:

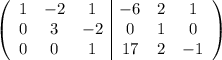
$\left(\begin{array}{ccc|ccc}1&-2&1&-6&2&1\\0&3&-2&0&1&0\\0&0&1&17&2&-1\end{array}\right)$

Прибавим ко второй строке 2 третьих и вычтем из первой третью:

$\left(\begin{array}{ccc|ccc}1&-2&0&-23&0&2\\0&3&0&34&5&-2\\0&0&1&17&2&-1\end{array}\right)$

Делим вторую строку на 3:

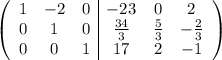
$\left(\begin{array}{ccc|ccc}1&-2&0&-23&0&2\\0&1&0&\frac{34}{3} &\frac{5}{3}&{-\frac{2}{3}}\\0&0&1&17&2&-1\end{array}\right)$

Прибавляем в первой строке 2 вторых:

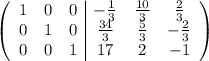
$\left(\begin{array}{ccc|ccc}1&0&0&{-\frac{1}{3}}&\frac{10}{3}&\frac{2}{3}\\0&1&0&\frac{34}{3} &\frac{5}{3}&{-\frac{2}{3}}\\0&0&1&17&2&-1\end{array}\right)$

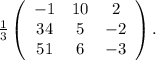
$\frac{1}{3}\left(\begin{array}{ccc}-1&10&2\\34&5&-2\\51&6&-3\end{array}\right).$

4,8(27 оценок)

Ответ:

polina359674

14.02.2023

А) 3х -2у =8 ⇒ 2у = 3х -8 ⇒ у = 1,5 х -4
В этом уравнении угловой коэффициент к = 1,5.
Любое уравнение , в котором к≠ 1,5 будет иметь единственное решение с данным
(у = 2х +8; у = -2х +6 и т.д.)
б) -5х +4у =3 ⇒ 4у = 3х -8 ⇒ у = 5 х +3
В этом уравнении угловой коэффициент к = 5.
Любое уравнение , в котором к≠ 5 будет иметь  единственное решение с данным
(у = 2х +8; у = -2х +6 и т.д.)
в) -3х -7 у =2 ⇒ 7у = -3х - 2 ⇒ у = -3/7 х -  2/7
В этом уравнении угловой коэффициент к = -3/7
Любое уравнение , в котором к≠ -3/7 будет иметь  единственное решение с данным
(у = 2х +8; у = -2х +6 и т.д.)
г)5х + 6у = 9 ⇒ 6у = -5х - 9 ⇒ у = -5/6 х - 9/6
В этом уравнении угловой коэффициент к =-5/6.
Любое уравнение , в котором к≠ -5/6 будет иметь  единственное решение с данным
(у = 2х +8; у = -2х +6 и т.д.)

4,7(92 оценок)

Это интересно:

Компьютеры-и-электроника

29.01.2021

Как легко изменить свой идентификатор Apple ID...

Мир-работы

19.10.2021

Как отменить собеседование на работу и не потерять репутацию...

Здоровье

09.08.2022

Как избавиться от круглых щек: эффективные советы для вас...

Транспорт