на нуль делить нельзя
число в модуле не может быть отрицательным
Объяснение:
например
1) при х=-8
если отрицательное значение записать в модуле то оно станет положительным и таким образом 8:(-8)=-1
2) при х=-5
если отрицательное значение записать в модуле то оно станет положительным и таким образом 5:(-5)=-1
3) при х=1
число изначально положительное и поэтому если записать его в модуле то его значение не изменится т.е он так и будет оставаться 1
1:1=1
4) при х=7
число изначально положительное и поэтому если записать его в модуле то его значение не изменится т.е он так и будет оставаться 7
7:7=1
5) при х=128
число изначально положительное и поэтому если записать его в модуле то его значение не изменится т.е он так и будет оставаться 128
128:128=1
6) при х больше нуля
в таком случае нам надо взять самое наименьшее число которое больше нуля т.е это число 1 исходя от этого получается что 1:1=1 (можно взять другие числа)
надеюсь что
хорошего дня
x^2-6x+19=0
a=1 b=-6 c=19
D=b^2-4ac=(-6)^2-4*1*19=36-76<0, следовательно, решений нет. ответ: решений нет.
x^2-6x+9=0
a=1 b=-6 c=9
D=b^2-4ac=(-6)^2-4*1*9=36-36=0, следовательно, ур-е имеет единственный корень, который мы можем вычислить по формуле: x=(-b)/2a=-(-6)/2*1=6/2=3 ответ: 3.
x^2-6x=0
Вынесем "х" за скобку:
x(x-6)=0
Произведение равно 0 тогда, когда хотя бы один из множителей равен 0. Следовательно:
x=0 или x-6=0 x=6 ответ: 0, 6.
x^2-6=0
x^2=6
Извлекаем квадратный корень из двух частей и получаем:
![x=\sqrt[2]{6} \\x=-\sqrt[2]{6}](/tpl/images/4424/0353/fa5da.png)
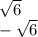
Объяснение:
........................