Еще одна популярная задача теории вероятностей (наравне с задачей о подбрасывании монет) - задача о подбрасывании игральных костей.
Обычно задача звучит так: бросается одна или несколько игральных костей (обычно 2, реже 3). Необходимо найти вероятность того, что число очков равно 4, или сумма очков равна 10, или произведение числа очков делится на 2, или числа очков отличаются на 3 и так далее.
Основной метод решения подобных задач - использование формулы классической вероятности, который мы и разберем на примерах ниже.
Ознакомившись с методами решения, вы сможете скачать супер-полезный Excel-файл для расчета вероятности при бросании 2 игральных костей (с таблицами и примерами).
Объяснение:
если не по теме то не баньте
1) 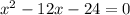

данное уравнение имеет два различных корня.
по теореме Виета:
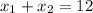

Т.к. произведение корней отрицательно, то два корня разных знаков: меньший - отрицательный, больший - положительный.
2) 

уравнение имеет два различных корня.
по теореме Виета:
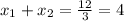
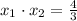
Т.к. произведение корней положительно, то имеет два корня одного знака, а т.к. сумма корней положительна, то имеет два положительных корня.
3) 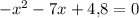
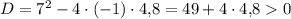
уравнение имеет два различных корня. По т. Виета:
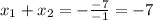
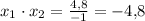
Т.к. произведение корней отрицательно, то имеет два корня различных знаков: меньший - отрицательный, больший - положительный.
4) 

уравнение имеет два различных корня. По т. Виета:
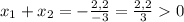
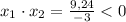
Т.к. произведение корней отрицательно, то имеет два корня разных знаков: меньший - отрицательный, больший - положительный.
если графики пересекаютя, то их части с х равны:
-27x + 1 = ?x + ?
При этом они пересекаются в точке (0; 1), значит х = 0, а у = 1
Подставив эти значения в известное уравнение получим:
1 = -27 * 0 + 1
Таким образом мы выяснили, что на месте первого вопроса может стоять любое число (так как х = 0, а 0 умножить на любое число, всё равно будет 0), а на месте второго -- обязательно 1.
Например:
y = 5x + 1