Будь ласка до іть терміново. Дуже . Дякую

Question

Алгебра: Будь ласка до іть терміново. Дуже . Дякую

амоооооооо · Accepted Answer

Из 9 солдат нужно выбрать некоторых 7. Число сделать это равно числу сочетаний из 9 элементов по 7:

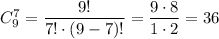
$C_9^7=\dfrac{9!}{7!\cdot(9-7)!} =\dfrac{9\cdot8}{1\cdot2} =36$

Из 6 сержантов нужно выбрать некоторых 4. Число сделать это равно числу сочетаний из 6 элементов по 4:

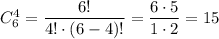
$C_6^4=\dfrac{6!}{4!\cdot(6-4)!} =\dfrac{6\cdot5}{1\cdot2} =15$

Из 4 офицеров нужно выбрать некоторого 1. Число сделать это равно числу сочетаний из 4 элементов по 1:

C_4^1=4

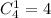
Так как выбор солдат, выбор сержантов и выбор офицера попарно независимы, то соответствующие нужны перемножить. То есть любому выбору солдат мы можем сопоставить любой выбор сержантов, а также любой выбор офицера.

Общее число вариантов:

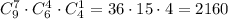
$C_9^7\cdot C_6^4\cdot C_4^1=36\cdot15\cdot4=2160$

ответ: 2160 вариантов

MOGZ ответил