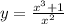
Для числа 18 ответ: да, можно.
Я рассуждал так:
если меняется только одна цифра, значит, меняется только один разряд числа: единицы, десятки, сотни и т.д.
• Изменяя только единицы, деление на 18 снова не получится. Потому что от одного числа, которое делится на 18, до другого должна быть разница хотя бы в эти самые 18.
• Изменяя десятки, мы делаем предположение, что какое-либо круглое двузначное число делится на 18, и это так:
90 : 18 = 5.
Таким образом, если найдётся число, у которого в разряде десятков стоит 0, и оно делится на 18, достаточно будет заменить 0 на 9, чтобы получить новое число, делящееся на 18.
Пример: 108 и 198.
Для числа 19 ответ: нет, нельзя.
Рассуждения аналогичные, только в десятках умножение 19 ни на какое число не даст круглого двузначного числа. То же самое и с сотнями, и с тысячами и т.п., ведь из девятки на конце может получиться нуль только умножением на 10, или кратное ему, а это нам не подходит, т.к. числа 190 и подобные ему будут изменять не один разряд числа, а несколько. Так что только одну цифру изменить никак не получится.
Теперь приводим дроби к одному знаменателю, который в данном случае будет равен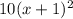
. Для этого первую дробь мы домножаем на 10, вторую дробь - на 
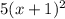, а третью - на 
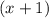. Получаем:
Дробь равна нулю, когда числитель равен нулю, а знаменатель отличен от нуля. То есть:
Приравняем числитель к нулю с учётом нашего условия:
Таким образом, наше уравнение имеет два решения. Но по условию нас просят отобрать только целые решения. Наш первый корень, 4, принадлежит множеству целых чисел, в то время, как второй корень,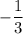
, целым числом не является. Таким образом, в ответ пойдёт только 
.
ответ: 4.