х≠ℝ
Объяснение:
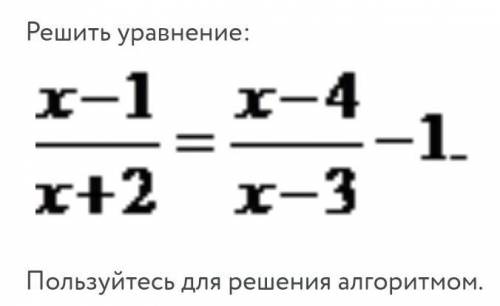
Итак. Найдем область допустимых значений
Х-1/х+2=х-4/х-3=-1, следовательно х≠-2 , х≠3
Переместим выражение в левую часть и изменим его знак
Х-1/х+2 - х-4/х-3 + 1 = 0
Запишем все числителели под одним общим знаменителем. (Х+2)*(х-3)
(Х-3)*(х-1)-(х+2)*(х-4)+(х+2)*(х-3) / (х+2)*(х+3) = 0
Перемножим выражения в скобках
х²-х-3х+3-(х+2)*(х-4)+(х+2)*(х-3) / (х+2)*(х+3) = 0
Затем
х²-х-3х+3-(х²-4х+2х-8)+(х+2)*(х-3) / (х+2)*(х+3) = 0
Затем
х²-х-3х+3-(х²-4х+2х-8)+х²-3х+2х-6/(х+2)*(х+3) = 0
Приведем подобные члены:
х²-х-3х+3-х²-2х-8+х²-3х+2х-6/(х+2)*(х+3) = 0
Следовательно из этого получаем следующее, ведь перед нашими скобками стоит знак. Значит мы изменим знак каждого члена в скобках.
х²-х-3х+3-х²+2х+8+х²-3х+2х-6/(х+2)*(х+3) = 0
А поскольку сумма двух противоположных величин
Равна нулю , удалим их из выражения.
-х-3х+3+2х+8+х²-3х+2х-6/(х+2)*(х+3) = 0
Приведем подобные члены:
-3х+3+8+х²-6/(х+2)*(х-3) = 0
Вычислим сумму и разность:
-3х+5+х²/(х+2)*(х-3) =0
Когда частное выражений равно нулю, то и числитель должен быть равен нулю. Значит
-3х+5+х²=0
Используя переместительный закон Изменим порядок членов.
х²-3х-5=0
Решим квадратное уравнение используя формулу.
Х= -(-3)±√(это знак квадратного корня, его продолжай до конца уравнения) (-3)²-4*5(тут заканчивай квадратный корень) / 2х+1
Любое выражение умноженное на 1 не изменится.
Х= -(-3)±√(это знак квадратного корня, его продолжай до конца уравнения) (-3)²-4*5(тут заканчивай квадратный корень) / 2
А когда перед скобками стоит знак,
По правилу изменим знак каждого члена в скобках.
Х= 3±√(это знак квадратного корня, его продолжай до конца уравнения) (-3)²-4*5(тут заканчивай квадратный корень) / 2
Вычислим степень:
Х= 3±√(это знак квадратного корня, его продолжай до конца уравнения) 9-4*5(тут заканчивай квадратный корень) / 2
И умножим числа.
Х= 3±√(это знак квадратного корня, его продолжай до конца уравнения) 9-20(тут заканчивай квадратный корень) / 2
Вычислим разность:
Х= 3±√-11/2(2 без корня)
А так как корень из отрицательного числа не существует на множестве действительных чисел, то
х≠ℝ
это значит что Дискриминант отрицательный, значит нет решения.
Что и требовалось доказать!
Так же начертил график. Держи данные:
Корень (1,0)
Область определения: х≠-2
Пересечение с осью ординат
(0, - 1/2)
Область определения (вторая)
Х≠3
Пересечение с осью ординат:
(0, 1/3)
Найдем решения неравенства Ix-5I≤2; -2≤х-6≤2; 4≤х≤8- отрезок длиной 4
Найдем решения неравенства Ix-6I≥1
x-6≥1; х≥7 или х-6≤-1; х≤5; т.е. х∈(-∞;5]∪[7;8]
Из отрезка [4;8] выпадает только отрезок[5;7] длины 2
Используя геометрическое определение вероятности, найдем искомую вероятность, длина решений второго неравенства, которое находится в первом, составляет 2, это сумма длин отрезков [4;5] и [7;8], т.е. число благоприятствующих исходов равно 2, а общее число исходов 4, значит, вероятность равна 2/4=0.5
Чтобы найти НОД чисел нужно разложить их на простые множители и перемножить между собой общие множители (подчёркнуты).
Чтобы сократить дробь, нужно числитель и знаменатель разделить на НОД.
1) 24 = 2 * 2 * 2 * 3
60 = 2 * 2 * 3 * 5
НОД (24; 60) = 2 * 2 * 3 = 12
2) 45 = 3 * 3 * 5
105 = 3 * 5 * 7
НОД (45; 105) = 3 * 5 = 15
3) 39 = 3 * 13
130 = 2 * 5 * 13
НОД (39; 130) = 13
4) 64 = 2 * 2 * 2 * 2 * 2 * 2
144 = 2 * 2 * 2 * 2 * 3 * 3
НОД (64; 144) = 2 * 2 * 2 * 2 = 16
Чтобы найти НОК чисел, нужно разложить их на простые множители и к множителям бОльшего числа добавить недостающие множители (подчёркнуты) и перемножить их между собой.
Наименьшее общее кратное и будет наименьшим общим знаменателем.
1) 12 = 2 * 2 * 3
8 = 2 * 2 * 2
НОК (12; 8) = 2 * 2 * 3 * 2 = 24
2) 9 = 3 * 3
15 = 3 * 5
НОК (9; 15) = 3 * 5 * 3 = 45
3) 25 = 5 * 5
15 = 3 * 5
НОК (25; 15) = 5 * 5 * 3 = 75
4) 16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3
НОК (16; 24) = 2 * 2 * 2 * 3 * 2 = 48
Дискриминант отрицательный, значит нет решения.
ответ: Нет решения.