В условии задачи нам дана информация о скорости велосипедиста и мотоциклиста, а также общая длина пути между городами А и Б, которая равна 120 км.
Для начала, давайте найдем время, которое потратит велосипедист и мотоциклист на дорогу между городами А и Б.
Для велосипедиста:
Время = Дистанция / Скорость = 120 / (10 км/ч) = 12 часов.
Для мотоциклиста:
Время = Дистанция / Скорость = 120 / (10 км/ч + х км/ч), где х - разность скоростей мотоциклиста и велосипедиста.
Теперь нам нужно найти значение х. Для этого воспользуемся информацией из условия задачи: скорость велосипедиста на 10 км/ч меньше, чем скорость мотоциклиста.
Пусть скорость мотоциклиста будет V км/ч. Тогда V - 10 км/ч - скорость велосипедиста.
Теперь мы можем записать уравнение:
120 = (10 км/ч + V) * Время (в часах).
Подставляем значение времени (12 часов):
120 = (10 км/ч + V) * 12.
Раскрываем скобки:
120 = 120 км/ч + 12V.
Вычитаем 120 км/ч из обеих сторон уравнения:
0 = 12V.
V = 0 км/ч.
Таким образом, получаем, что скорость мотоциклиста V = 0 км/ч.
Ответ: скорость мотоциклиста равна 0 км/ч.
Обратите внимание, что это странное решение, поскольку получается, что мотоциклист стоит на месте и не движется. Возможно, в оригинальной задаче есть ошибки или опечатки.
Но при условии, что скорость мотоциклиста равна 0 км/ч, он перемещается со скоростью, равной 0 км/ч.
Хорошо! Давайте начнем с построения графика уравнения х²+ 1/4y²= 4.
1. Для начала, мы должны выразить y из данного уравнения. Для этого, давайте умножим всю сторону уравнения на 4, чтобы избавиться от дроби:
4 * (х²+ 1/4y²) = 4 * 4
4x² + y² = 16
2. Затем, давайте выразим y в квадрате:
y² = 16 - 4x²
3. Теперь возьмем квадратный корень от обеих сторон уравнения, чтобы получить y отдельно:
√(y²) = √(16 - 4x²)
y = ±√(16 - 4x²)
4. Когда значение y выбирается, оно может быть положительным или отрицательным. Будем строить график обоих случаев, чтобы увидеть полное изображение.
5. Теперь, давайте построим таблицу значений для х и y. Выберем несколько значений для х, рассчитаем соответствующие значения для y и запишем их:
V=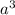
Это формула! Та которая вам нужна)