Привет. Данная тема очень простая.
Ты наверное знаешь, что такое степень.
Степень - умножение на самого себя
Чему ровна степень, столько раз число умножается на само себя.
Пример:
2 ² = 4
6² = 36
4² = 16
Степень также пишут вот так ^2
Так вот, Есть некоторые правила, которые надо запомнить.Свойства степеней
a^n * a^m = a^(a+m)
a^n : a^m = a^(a-m)
(a^n)^m = a^(n*m)
(ab)^n = a^n*b^n
Эти правила записать или расписать произведения чисел в степени по разному
ответ:x^2 * x^3 = x^(2+3) = x^5
Вот и все, просто)
Если тебе ничего не понятно, то держи ссылки.
https://skysmart.ru/articles/mathematic/svojstva-stepenej
stepenejhttps://images.slideplayer.com/16/5141786/slides/slide_6.jpg
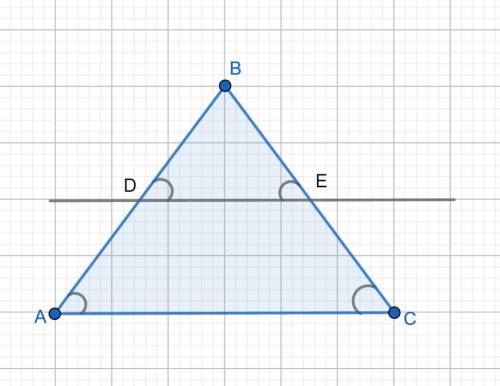
Можно доказать несколькими По т. Фалеса: Если параллельные прямые отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на второй стороне угла.
Параллельные прямые DE и AC отсекают равные отрезки на стороне AB угла ABC, т.е. AD = DB. Значит на стороне BC они отсекают также равные отрезки BE = EC.
2) Из подобия треугольников. Так как DE ║ AC, то ΔABC подобен ΔDBE по двум углам: ∠B общий, ∠BDE = ∠BAC как соответствующие при DE ║ AC и секущей AB. Так как по условию AD = DB, то BD/AB = 1/2. Коэффициент подобия k = 1/2. ⇒ BE/BC = 1/2, ⇒ BC = 2*BE, тч. E является серединой отрезка ВС.
3) Проведем прямые BO ║AC и ON║AB.
DBON параллелограмм, так как его противолежащие стороны параллельны. ⇒ DB = EO. ADEN параллелограмм, так как его противолежащие стороны параллельны, так как AD=DB, то NE=EO.
ΔBEO = ΔNEC по второму признаку: ∠BEO = NEC вертикальные, ∠BOE = ∠ENC внутренние накрест лежащие при BO ║AC и секущей ON. OE = EN. Из равенства треугольников следует BE=EC. ( так доказывается т. Фалеса)
Объяснение:
80=16∗5=16∗5=45
ну думаю жол правильнр