1) x = ±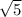
2) y =± 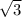
3) z = ±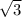
4) k = ±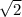
5) x1 = ±1; x2 = ±3
6) y = ±1
7)t1 = ±1; t2 = ±2
8)x1 = ±3; x2 = ±0.5
Объяснение:
1) x^4 - x^2 - 20 = 0
Замена x^2 = t >0
t^2 - t - 20 = 0
D = 1 + 4*20 = 81 = 9^2
t1 = (1 + 9)/2 = 5
t2 = (1 - 9)/2 = -4 - посторонний
Обратная замена
x^2 = 5
x = ±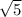
2)y^4 - 6y^2 + 9 = 0
Замена y^2 = t >0
t^2 - 6t + 9 = 0
D = 36 - 4*9 = 0
t = (6 ± 0)/2 = 3
Обратная замена
y^2 = 3
y = ± 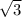
3) z^4 - z^2 - 6 = 0
Замена z^2 = t >0
t^2 - t - 6 = 0
D = 1 + 4*6 = 25 = 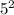
t1 = (1 + 5)/2 = 3
t2 = (1 - 5)/2 = -2 - посторонний
Обратная замена
z^2 = 3
z = ±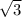
4) x^4 - 10x^2 + 9 = 0
Замена x^2 = t >0
t^2 - 10t + 9 = 0
т.к. a + b + c = 0
t1 = 1
t2 = 9
Обратная замена
x^2 = 1 или x^2 = 9
x1 = ±1
x2 = ±3
4) k^4 + 5k - 14 = 0
Замена k^2 = t >0
t^2 + 5t - 14 = 0
D = 25 + 4*14 = 81
t1 = (-5 + 9)/2 = 2
t2 = (-5 - 9)/2 = -7 - посторонний
Обратная замена
k^2 = 2
k = ±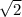
6) 49y^4 - 48y^2 - 1 = 0
Замена y^2 = t >0
49t^2 - 48t - 1 = 0
т.к. a + b + c = 0
t1 = 1
t2 = -1 - посторонний
Обратная замена
y^2 = 1
y = ±1
7) t^4 - 5t^2 + 4 = 0
Замена t^2 = x >0
x^2 - 5x + 4 = 0
т.к. a + b + c = 0
x1 = 1
x2 = 4
Обратная замена
t^2 = 1 или t^2 = 4
t1 = ±1
t2 = ±2
8) 4x^4 - 37x + 9 = 0
Замена x^2 = t >0
4t^2 - 37t + 9 = 0
D = 1369 - 4*4*9 = 35²
t1 = (37 + 35)/8 = 9
t2 = (37 - 35)/8 = 0.25
Обратная замена
x^2 = 9 или x^2 = 0.25
x1 = ±3
x2 = ±0.5
1) (a - b)² = a² - 2ab + b²
(2х - 1)² = 16
(2х)² - 2 · 2х · (-1) + (-1)² = 16
4х² + 4х + 1 - 16 = 0
4х² + 4х - 15 = 0
D = b² - 4ac = 4² - 4 · 4 · (-15) = 16 + 240 = 256
√D = √256 = 16
х₁ = (-4-16)/(2·4) = (-20)/8 = -2,5
х₂ = (-4+16)/(2·4) = 12/8 = 1,5
ответ: (-2,5; 1,5).
3) (a + b)² = a² + 2ab + b²
25 - (5х + 1)² = 0
25 - ((5х)² + 2 · 5х · 1 + 1²) = 0
25 - (25х² + 10х + 1) = 0
25 - 25х² - 10х - 1 = 0 (умножим обе части уравнения на (-1))
25х² + 10х + 1 - 25 = 0
25х² + 10х - 24 = 0
D = b² - 4ac = 10² - 4 · 25 · (-24) = 100 + 2400 = 2500
√D = √2500 = 50
х₁ = (-10-50)/(2·25) = (-60)/50 = -1,2
х₂ = (-10+50)/(2·25) = 40/50 = 0,8
ответ: (-1,2; 0,8).
Объяснение: