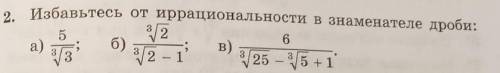
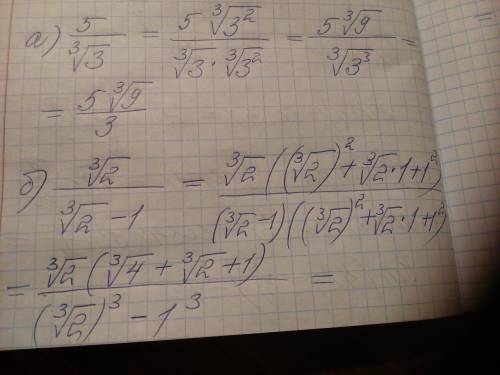

1. ![\dfrac{5}{\sqrt[3]{3}}=\dfrac{5\sqrt[3]{9}}{\sqrt[3]{27}}=\dfrac{5\sqrt[3]{9}}{3}.](/tpl/images/2061/3105/a992c.png)
2. ![\dfrac{\sqrt[3]{2}}{\sqrt[3]{2}-1}=\dfrac{\sqrt[3]{2}(\sqrt[3]{4}+\sqrt[3]{2}+1)}{(\sqrt[3]{2}-1)(\sqrt[3]{4}+\sqrt[3]{2}+1)}=\dfrac{2+\sqrt[3]{4}+\sqrt[3]{2}}{2-1}=2+\sqrt[3]{4}+\sqrt[3]{2.}](/tpl/images/2061/3105/ff5b9.png)
3. ![\dfrac{6}{\sqrt[3]{25}-\sqrt[3]{5}+1}=\dfrac{6(\sqrt[3]{5}+1)}{(\sqrt[3]{5}+1)(\sqrt[3]{25}-\sqrt[3]{5}+1)}=\dfrac{6(\sqrt[3]{5}+1)}{5+1}=\sqrt[3]{5}+1.](/tpl/images/2061/3105/72108.png)
Замечание. Мы использовали формулы
 и .
и . 
Подробное объяснение: в задании номер 1 число 3 в 4 степени возводится в 5 степень. Когда ты видишь что-то наподобие этого, то степени перемножаются: то есть 4 степень умножаем на 5 степень и получаем 20 степень, то есть 3 в 20 степени. Далее, в числителе, видим:
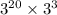
Здесь степени тоже умножаюся, потому что умножаются сами числа. Перемножаем и получаем 3 в 23 степени. Ну и затем остается сократить то, что получилось:
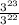
Сокращаем и получаем:
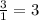
Задание номер 2.
Ну, тут все просто, тут надо правильно перемножить, как на фото. С умножением степеней ситуация та же, что и в 1 задании.
Надеюсь
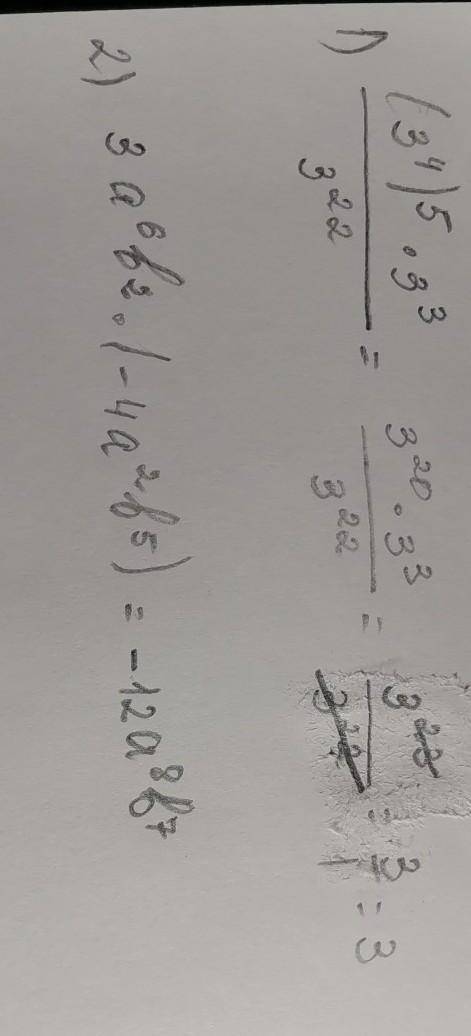
Объяснение:
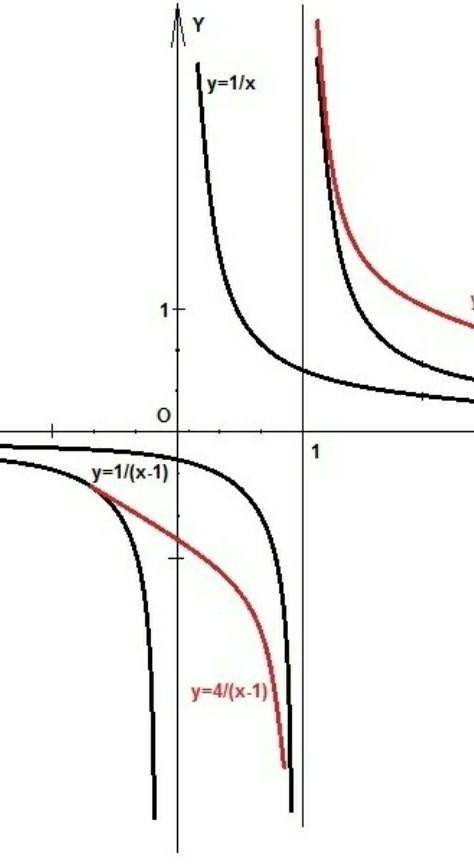
У нас есть график y = 1/x.
1) Чтобы получить y = 1/(x-1), его нужно сдвинуть на 1 вправо.
Теперь вертикальная линия разрыва будет x = 1, а не x = 0.
Чтобы получить y = 4/(x-1), нужно все значения умножить на 4.
2) Точно также, сначала сдвигаем график y = 1/x на 2 влево, а потом переворачиваем график и умножаем все значения на 3.
3) Тоже, сначала сдвигаем график y = 1/x на 1 вправо, потом умножаем все значения на 2, и, наконец, сдвигаем весь график на 3 вверх.
1 график я нарисовал на рисунке, остальные делаются точно также.
Но это очень приблизительный график, точнее в Пайнте не построишь.
Главное, понятен порядок построения.