Это хорошо понять , используя свойство пропорции: произведение крайних членов равно произведению крайних членов пропорции, то есть:
Мы видим, что в двух случаях были разные пропорции, но, применив свойство, получили одинаковые равенства. Значит одна пропорция следует из другой. Вообще, так как от перемены мест сомножителей произведение не меняется, то МНОЖИТЕЛИ , стоящие в числителе одной дроби, можно переносить в знаменатель другой дроби , всё равно произведение числителя одной дроби и знаменателя другой дроби будет одинаковым. Если есть целое, а не дробное выражение, то его всегда можно представить, как дробь со знаменателем 1.
Объяснение:
По определению функции синус: -1 ≤ sin x ≤ 1
По условию: sin x = 4a - a² - 5 ⇒ -1 ≤ 4a - a² - 5 ≤ 1
Проверим точку a = 2 для неравенства: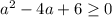
Следовательно при a = 2 система неравенство -1 ≤ 4a - a² - 5 ≤ 1 имеет решение.