Решение:
Любое натуральное число N представимо в виде произведения
N = (p1k1)*(p2k2)*... и т.д.,
где p1, p2 и т.д. - простые числа, а k1, k2 и т.д. - целые неотрицательные числа.
Например,
15 = (31)*(51)
72 = 8*9 = (23)*(32)
Так вот, общее количество натуральных делителей числа N равно
(k1+1)*(k2+1)*...
Итак, по условию, P = N1*N2*...*N11, где
N1 = (p1k[1,1])*(p2k[1,2])*...
N2 = (p1k[2,1])*(p2k[2,2])*...
...,
а это значит, что
P = (p1(k[1,1]+k[2,1]+...+k[11,1]))*(p2(k[1,2]+k[2,2]+...+k[11,2]))*...,
и общее количество натуральных делителей числа P равно
(k[1,1]+k[2,1]+...+k[11,1]+1)*(k[1,2]+k[2,2]+...+k[11,2]+1)*...
Это выражение принимает минимальное значение, если все числа N1...N11 являются последовательными натуральными степенями одного и того же простого числа, начиная с 1: N1 = p, N2 = p2, ... N11 = p11.
То есть, например,
N1 = 21 = 2,
N2 = 22 = 4,
N3 = 23 = 8,
...
N11 = 211 = 2048.
Тогда количество натуральных делителей числа P равно
1+(1+2+3+...+11) = 67.
Пусть х (руб) стоит 1 м шерсти, тогда у (руб) стоит 1 м шелка. Сниженная цена за 1 метр шерсти будет 0,75 х (руб), а сниженная цена за 1 метр шелка 0,85 у (руб.) Составим систему уравнений.
5х+4у=1600
5*0,75х+5*0,85у=1537,5
х=(1600-4у)/5
3,75х+4,25у=1537,5
Подставим значение х из первого уравнения во второе
3,75*((1600-4у):5)+4,25у=1537,5
(6000-15у):5+21,25у=7687,5
Избавимся от знаменателя, домножив всё на 5
6000-15у+4,25у*5=1537,5*5
6000-15у+21,25у=7687,5
6,25у=1687,5
у=1687,5:6,25
у=270
5х+4*270=1600
5х+1080=1600
5х=520
х=104
ответ: 1 метр шелка стоит 270 руб., а 1 метр шерсти - 104 руб
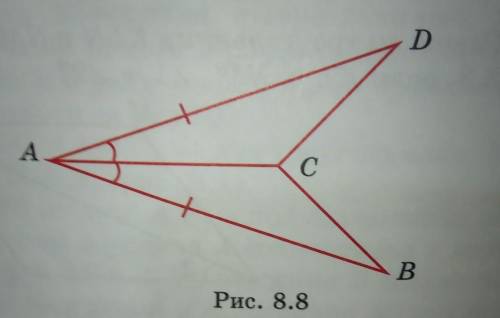
AC - общая сторона для треугольников BAC и DAC, AB и AD равны, ∠BAC = ∠DAC ⇒ ΔBAC = ΔDAC по двум сторонам и углу между ними