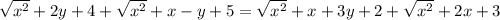
Объяснение:
1) найдем координаты вершины параболы по формуле
х₀=-b/2a
х₀=-6/(2(-1))=3
у₀=у(3)=-9+18-5=4
2) выразим х чрез у
y=-x²+6x-5
x²-6x+(y+5)=0 это квадратное уравнение решаем его по фрмуле корней
x₁₋₂=(-b±√d)/2a=(6±(√(36-4(у+5))))/2=(6±(√4(9-4(у+5))))/2=
=(6±2(√(9-(у+5))))/2=3±√(9-(у+5))=3±√(9-у-5)=3±√(4-у)
получилось 2 выражения
х=3+√(4-у)
х=3-√(4-у)
3) меняем местами х и у
y=3+√(4-x)
y=3-√(4-x)
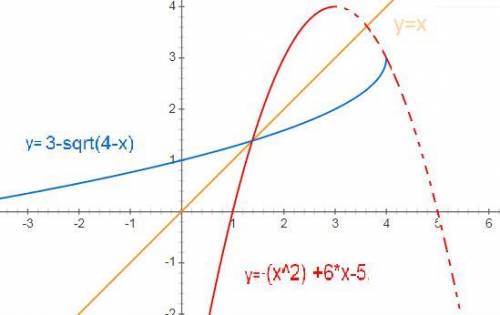
c учетом того, что графики прямой и обратной функции симметричны относительно прямой у=х
для х∈(-∞;3] обратной функцией будет y=3-√(4-x)
Дополнительно
график прямой и обратной функции
1 формула сложения
Cos (x+п/6) = cosx * cos(п/6) – sinx*sin(п/6)=1/2 cosx - √3/2sinx
2 формула двойного угла
Sinx=4/5 ; cos2x = 1- sin2x = 1-(4/5)2 =1-16/25=9/25 ; cosx =3/5
Sin2x = 2*sinx*cosx =2*4/5*3/5=24/25
3 формула двойного /тройного угла
-sina /(sin2a*sin3a) =
=-sin(3a-2a) /(sin2a*sin3a) =
=- (ctg2a – ctg3a) = ctg3a – ctg2a
4 11x =8x+3x ; 5x =8x -3x
sin11x +sin5x =2*1/2 (sin(8x+3x)+sin(8x-3x)) =2*sin8x*cos3x
5 формула двойного угла
(ctg^2(п/8)-1) / (2ctg(п/8)) = ctg (2*п/8) = ctg (п/4)=ctg 45o =1