Решением данной системы является пара чисел: 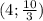 .
.
Объяснение:
Перед нами система уравнений с двумя неизвестными:
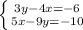
Данную систему уравнений проще решить, используя метод исключения одной переменной. Для этого домножим обе части первого уравнения на 3:
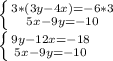
Теперь, сложим оба уравнения данной системы, чтобы избавиться от переменной y. Найдем x, путем упрощения обычного уравнения:
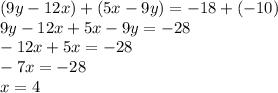
Теперь подставим данное значение в первое уравнение системы, чтобы найти y:
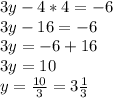
Получили ответ, что решением данной системы является пара чисел: 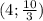
Найдем значение выражения 9 1/6 : (4 1/3 - 8) + 24 * 3/8.
Сначала в порядке очереди находим значение выражения в скобках, затем вычисляем умножение или деление, потом проводятся действия сложения или вычитания. То есть получаем:
9 1/6 : (4 1/3 - 8) + 24 * 3/8 = (9 * 6 + 1)/6 : (4 + 1/3 - 8) + 24 * 3/8 = (54 + 1)/6 : (- 4 + 1/3) + 24 * 3/8 = 55/6 : (- 3 - 3/3 + 1/3) + 3 * 8 * 3/8 = 55/6 : (- 3 - 2/3) + 3 * 1 * 3/1 = 55/6 : (- 11/3) + 3 * 3 = - 55/6 : 11/3 + 3 * 3 = - 55/6 * 3/11 + 3 * 3 = - 11 * 5/(2 * 3) * 3/11 + 9 = 5/2 + 9 = 2,5 + 9 = 11,5;
ответ: 11,5.
1. √х = 1 (1)
Выражение под корнем всегда должно быть неотрицательным, значит, х ≥ 0. Теперь возводим в квадрат обе части уравнения (1):
х = 1, смотрим на неравенство, х = 1 ≥ 0, значит, х = 1 – решение уравнения.
2. √х = -х - 2 (2)
Делаем то же самое. Выражение под корнем должно быть неотрицательным, но также в правой части уравнения (2) есть переменная, и правая часть тоже принимает разные значения, но извлечение корня из неотриц. выражения – так же неотриц. значение. Поэтому нужно, чтобы два условия выполнялись одновременно, т.е. нужно составить систему неравенств:
х ≥ 0
-х - 2 ≥ 0 (все это в системе)
Отсюда:
х ≥ 0
х ≤ -2 (в системе)
Могут ли эти условия выполняться одновременно? Т.е. есть ли такой х = числу, которое больше нуля и меньше -2? Такого числа не существует, значит, решения уравнени не сущ., следует, х принадлежит пустому множеству.