
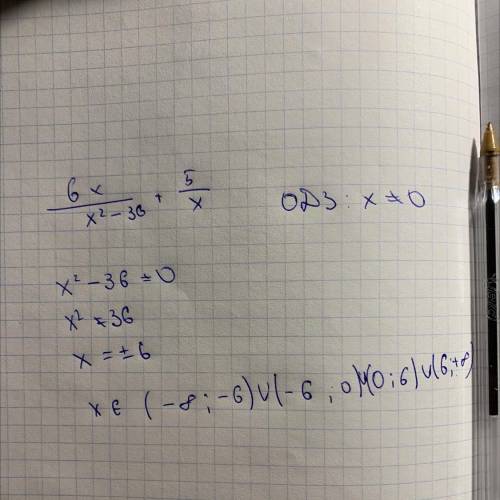
Целые числа называются взаимно простыми, если они не имеют никаких общих делителей, кроме ±1. Примеры: 14 и 25 взаимно просты, а 15 и 25 не взаимно просты (у них имеется общий делитель 5).
Наглядное представление: если на плоскости построить «лес», установив на точки с целыми координатами «деревья» нулевой толщины, то из начала координат видны только деревья, координаты которых взаимно просты.
8, 15 — не простые, но взаимно простые.
6, 8, 9 — взаимно простые числа, но не попарно взаимно простые.
8, 15, 49 — попарно взаимно простые.
Приравняем знаменатели к нулю
х²-36=0
х=0
Перенесём постоянную в правую часть и изменим её знак.
х²=36
извлечем квадратный корень из обеих частей уравнения. Не забывая об использовании положительных и отрицательных корней.
х=±6
Следовательно одно будет со знаком минус, другое со знаком плюс.
х=-6
х=6
х=0
Это и есть наши недопустимые значения для первоначального выражения.
х=-6, х=6, х=0