Объяснение:
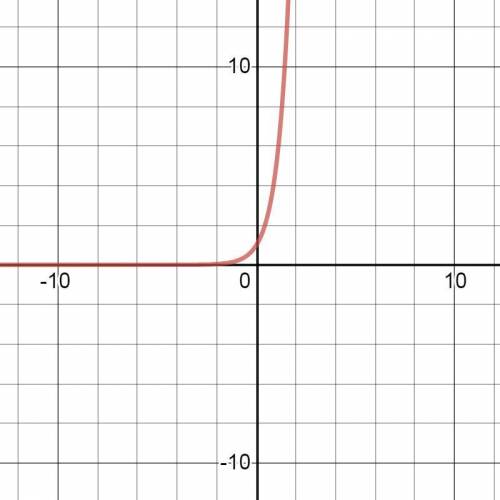
y=5ˣ.
Это показательная функция.
График этой функции показан на рис. 1.
Показательная функция y=5ˣ является строго монотонно возрастающей.
Область определения функции: х∈(-∞;+∞).
Область значений функции: у∈(0;+∞).
Точки пересечения с осью ОХ: нет.
Точки пересечения с осью ОУ: х=0 (0;1).
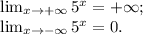
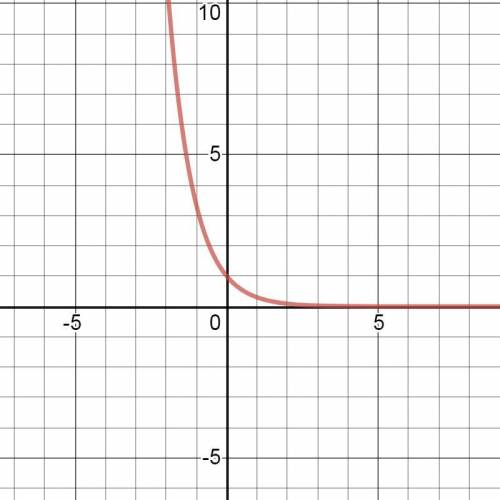
у=0,3ˣ
Это показательная функция.
График этой функции показан на рис. 2.
Показательная функция у=0,3ˣ является строго монотонно убывающей.
Область определения функции: х∈(-∞;+∞).
Область значений функции: у∈(0;+∞).
Точки пересечения с осью ОХ: нет.
Точки пересечения с осью ОУ: х=0 (0;1).
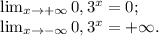
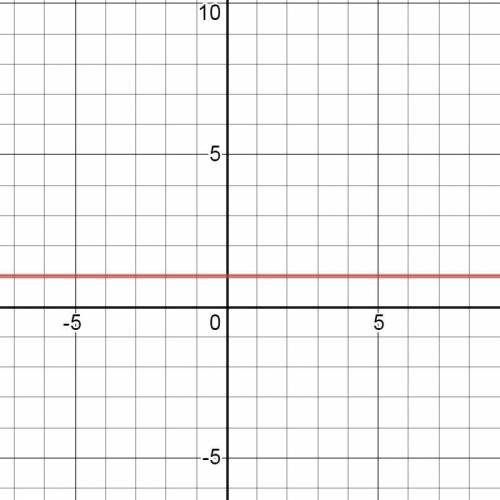
у=1ˣ.
График этой функции показан на рис. 3.
Единица в любой степени равена единице. ⇒
Получаем функцию у=1.
Графиком этой функции является график функции у=0 (ось ОХ),
смещённый вверх по оси ОУ на одну единицу.
Область определения функции: х∈(-∞;+∞).
Область значений функции: у=1.
Точки пересечения с осью ОХ: нет.
Точки пересечения с осью ОУ: х=0 (0;1).
2x+4=0
2х = -4
х = -4 ÷ 2
х = -2
ответ: -2.
(x+2)(x-1)=0
х^2 -х +2х -2 = 0
х^2 +х -2 = 0
D = 1 - 4×1×(-2) = 1 + 8 = 9>0
x1 = -1+3 / 2 = 2/2 = 1
x2 = -1-3 / 2 = -4/2 = -2
ответ: 1; -2.
x^2-4x=0
х(х-4) = 0
х = 0 и х-4 = 0
х = 4
ответ: 0; 4.
4z^2 - 4z +1 = 0
D = 16 - 4×4×1 = 16 - 16 = 0
z = 4 / 2×4 = 4/8 = 1/2 = 0,5
ответ: 0,5.
2(x-2) + x(x-2)=0
2х -4 + х^2 -2х = 0
х^2 -4 = 0
х^2 = 4
х1 = 2
х2 = -2
ответ: 2; -2.
x^2(x-3)(x+6) = 0
(х^3 -3х^2)×(х+6) = 0
х^4 +6х^3 -3х^3 -18х^2 = 0
х^4 + 3х^3 -18х^2 = 0
х^2(х^2 +3х -18) = 0
х^2 = 0 и
х^2 +3х -18 = 0
D = 9 - 4×1×(-18) = 9 + 72 = 81>0
x2 = -3+9 / 2 = 6/2 = 3
x3 = -3-9 / 2 = -12/2 = -6
ответ: 0; 3; -6.
Надеюсь