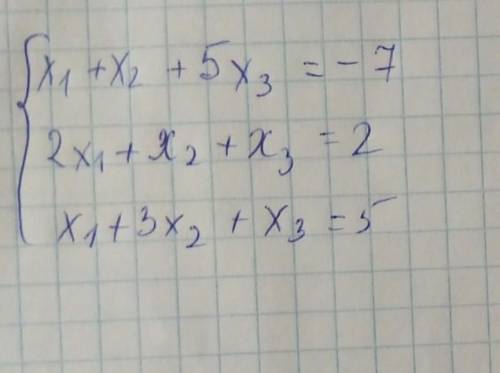


Первую строку оставляем без изменений. Вторую складываем с первой, умноженной на -2, результаты записываем во вторую. Из третьей строки вычитаем первую, результаты записываем в третью.
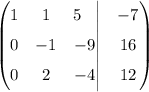
Первую и вторую строки оставляем без изменений. Третью складываем со второй, умноженной на 2, результаты записываем во вторую.

Переписываем третью строку в аналитическом виде.
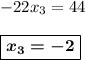
Значение одной переменной нашли. Переходим к следующей. Переписываем вторую строку в аналитическом виде.
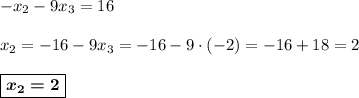
То же самое делаем с первой строкой.
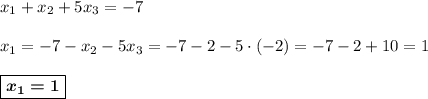
Нашли значения всех трёх переменных.
ответ: 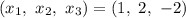 .
.
25
Объяснение:
решения.
Выпишем несколько первых натуральных чисел кратных 5:
5, 10, 15, 20, 25, 30, 35, 40, 54, ... (далее каждое пятое натуральное число будет являться членом данной последовательности).
Пронумеруем члены последовательности:

Число, следующее за четвертым членом последовательности 25.
решения.
Воспользуемся формулой для нахождения n-го члена арифметической последовательности.
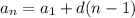
Наименьшее натуральное число делящееся на 5 это 5, т.е.  .
.
Далее каждое пятое натуральное число делится на 5. Значит разность арифметической прогрессии равна 5, т.е. 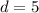 .
.
Т.к. по условию нужно найти число, следующее за a₄, то находим а₅.
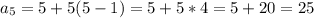
метод Гаусса
Объяснение: