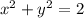
Объяснение:
Часть 1
1. Параллелограммом называется четырехугольник, у которого противолежащие стороны ...
1.параллельны
2.равны
3.пересекаются
4.перпендикулярны
2. Дайте название следующему утверждению: в параллелограмме противоположные стороны равны. 1.определение параллелограмма
2.признак параллелограмма
3.аксиома
4.свойство параллелограмма
3)В параллелограмме ABCD углу А противоположным будет угол ?
1. В
2. С
3. D
4. В параллелограмме нет противоположных углов
4. Какова сумма любых двух соседних углов в параллелограмме?
1) 180°
2) бывает разной
3) 270°
4) 90°
5. В четырехугольнике два противоположных угла равны. Является ли он параллелограммом?
1) не является
2) не обязательно
3) такая ситуация невозможна
4) является
6. Один из углов параллелограмма равен 35°. Чему равны остальные его углы?
1) 145°, 35°, 145°;
2) 55°, 125°, 5°;
3) 35°, 145°, 50.
Сумма двух соседних углов равна 180°, значит второй угол : 180 - 35= 145°. Противоположные углы в параллелограмме равны , значит оставшиеся углы : 145°;35°; 145°
7. Биссектрисы соседних углов параллелограмма:
1) перпендикулярны
2) параллельны
3) пересекаются и точкой пересечения делятся пополам
4) невозможно их провести
8. Продолжите: Биссектриса угла в параллелограмме отсекает от него равнобедренный треугольник.
9. Вставьте пропущенное слово: В параллелограмме противоположные стороны равны
10.Вставьте пропущенные слова: Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм
Часть 2 (задачи)
1.В параллелограмме АВСD биссектриса угла А пересекает сторону ВС в точке К так, что ВК = 7 см, КС = 3 см. Чему равен периметр параллелограмма?
Биссектриса угла в параллелограмме отсекает от него
равнобедренный треугольник, поэтому Δ АВК равнобедренный, значит АВ=ВК= 7 см
Сторона ВС=ВК+ КС= 7+3=10 см
Р=2*(АВ+ВС) =2*(10+7)=2*17 =34 см
ответ : Р= 34 см
( рис. 1 во вложении)
2. Из вершины В параллелограмма ABCD с острым углом А проведен перпендикуляр BK к прямой AD; ВК =1/2АВ. Найдите углы С и D
Рассмотрим Δ ABK. ( рис. 2) Он прямоугольный (∠ ВКА = 90°).
По условию BK = 1/ AB. А поскольку AB – гипотенуза Δ АВК ., то ∠ А = 30 ° (катет, лежащий против угла в 30 ° равен половине гипотенузы).
Поскольку в параллелограмме противолежащие углы равны, то
∠ С = 30 °
Теперь найдем ∠ D. В параллелограмме сумма внутренних углов равна 360 ° , значит
∠ D = ∠B = (360° - 2*30°):2= 150°.
ответ: C = 30 градусов, D = 150 градусов
( рис.2 во вложении)
1.
Тут легко выразить x из первого уравнения. Нужно лишь перенести 2y
x = -2y
Теперь подставляем это во второе
5(-2y) + y = -18
-9y = -18
y = 2
Помним, что x = -2y ===> x = -4
Для самопроверки можно подставить в первое, в других номерах делать не буду, но тебе советую (не конкретно в этих, а вообще)
-4 + 4 = 0 Все верно
x = -4; y = 2
2.
Здесь тоже легко выразить x из первого.
2x = 10 + 5y
Подставляем в первое, умножаем не на 4, а на 2, т.к. у нас уже 2x.
2(10 + 5y) - y = 2
20 + 10y - y = 2
18 = -9y
y = -2
Подставляем в 2x = 10 + 5y > 2x = 10 - 10 ===> x = 0
x = 0; y = -2
3. Тут конечно тоже можно выразить x и т.д., но ради разнообразия решим через алгебраическое сложение уравнений. Складываем все, что левее равно в первом, с тем, что левее равно во втором, ну и с тем, что правее соответственно. Знаки не меняем!
x - 2y + y - x = 1 - 2
-y = -1
y = 1
Теперь ищем x из первого.
x - 2 = 1
x = 3; y = 1
4. Тут тоже подойдет метод алгебраического сложения. Вообще, в этом номере все можно решить, выражая одну из переменных через метод алг-го сложения удобнее. Есть системы, где выразить переменную сложнее. Часто именно сложением или вычитание (это все метод алгебраического сложения) решить.
x + y + x - y = -3 - 1
2x = -4
x = -2
Подставляем в первое.
-2 + y = -3
y = - 1
x = -2; y = -1
Все. Если будут во пиши.
p.s. Отметь, как лучший, если не сложно ;)
z = x*y
1. Найдем частные производные.
2. Решим систему уравнений.
y = 0
x = 0
Получим:
а) Из первого уравнения выражаем x и подставляем во второе уравнение:
x = 0
y = 0
Откуда y = 0
Данные значения y подставляем в выражение для x. Получаем: x = 0
Количество критических точек равно 1.
M1(0;0)
3. Найдем частные производные второго порядка.
4. Вычислим значение этих частных производных второго порядка в критических точках M(x0;y0).
Вычисляем значения для точки M1(0;0)
AC - B2 = -1 < 0, то глобального экстремума нет.
Вывод: Глобального экстремума нет.