решение на фото00

Примем производительность первого маляра за х, второго за у
Тогда вдвоем они за 1 час покрасят
х+у=40 м²
Работая в одиночку, первый маляр покрасит 50 м² за
50:х (часов)
а второй 90м² за
90:у (часа)
Из условия задачи известно, что
90:у-50:х=4 (часа)
Составим систему уравнений:
|х+у=40
|90:у-50:х=4
Из первого уравнения найдем у через х
у=40-х
Подставим это значение во второе уравнение
90:(40-х)-50:х=4 Умножим обе части уравнения на х(40-х), чтобы избавиться от дроби.
90х-50(40-х)=4 х(40-х),
90х-2000 +50х =160х -4х²
4х² +90х-2000 +50х - 160х= 0
4х² -20х-2000=0 Для облегчения вычисления разделим обе части на 4, получим
х² -5х-500=0
Решая задачу через дискриминант, получим
х=25 м² в час
100 м² первый маляр покрасит за
100:25=4 часа.
Объяснение:
1) F(x) = √(4 - 5*x), Xo = 0
Y = F'(Xo)*(x - Xo) + F(Xo) - формула касательной.
Находим первую производную - k - наклон касательной.
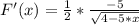
F'(Xo) = F'(0) = - 5/4 = k
F(0) = 2
y = - 5/4*x + 2 - касательная - ответ.
Задача 2)
ДАНО:Y(x) = x³ -3*x² + 2
ИССЛЕДОВАНИЕ.
1. Область определения D(y) ∈ R, Х∈(-∞;+∞) - непрерывная , гладкая.
2. Вертикальная асимптота - нет - нет разрывов.
3. Наклонная асимптота - y = k*x+b.
k = lim(+∞) Y(x)/x = +∞ - нет наклонной (горизонтальной) асимптоты.
4. Периода - нет - не тригонометрическая функция.
5. Пересечение с осью OХ.
Применим теорему Безу. х₁ *х₂ *х₃ = 2
Применим тригонометрическую формулу Виета.
Разложим многочлен на множители. Y=(x+0,73)*(x-1)*(x-2,73)
Нули функции: Х₁ =-0,73, Х₂ =1, Х₃ =2,73
6. Интервалы знакопостоянства.
Отрицательная - Y(x)<0 X∈(-∞;-0,73]U[1;2,73] Положительная -Y(x)>0 X∈[-0,73;1]U[2,73;+∞)
7. Пересечение с осью OY. Y(0) = 2
8. Исследование на чётность.
В полиноме есть и чётные и нечётные степени - функция общего вида.
Y(-x) ≠ Y(x) - не чётная. Y(-x) ≠ -Y(x), Функция ни чётная, ни нечётная.
9. Первая производная. Y'(x) = 3*x² -6*x = 0
Корни Y'(x)=0. Х₄ =0 Х₅=2
Производная отрицательна между корнями - функция убывает.
10. Локальные экстремумы.
Максимум - Ymax(X₄= 0) =2. Минимум - Ymin(X₅ = 2) =-2
11. Интервалы возрастания и убывания.
Возрастает Х∈(-∞;0;]U[2;+∞) , убывает - Х∈[0;2]
12. Вторая производная - Y"(x) = 6* x -6 = 0
Корень производной - точка перегиба Х₆=1
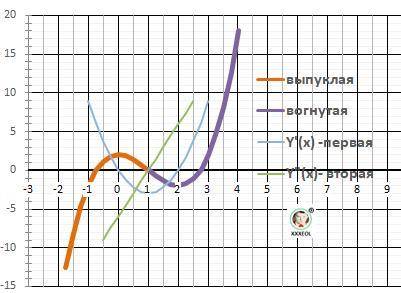
13. Выпуклая “горка» Х∈(-∞; Х₆ = 1]
Вогнутая – «ложка» Х∈[Х₆ = 1; +∞).
14. График в приложении.
Задача 3)
Ymin(0) = -3, Ymax(2) = 9 - ответ.
 : [tex]f(x)=\sqrt{4-5x} , x_{0} =0[/tex" />
: [tex]f(x)=\sqrt{4-5x} , x_{0} =0[/tex" />
Объяснение:
30x+18x²-15-9x-18x²+30x=87
51x=102
x=2