6. Определяет направление первого, второго, третьего и четвертого крестовых походов I - ми крестовый поход 1 крестовый поход Крестовый поход Крестовый поход IV крестовый поход
Задача: Два автомобиля выезжают одновременно из одного города в другой, находящийся на расстоянии 560 км. Скорость первого на 10 км больше скорости второго, и поэтому первый автомобиль приезжает на место на 1 час раньше другого. Определить скорость каждого автомобиля.
Пусть скорость второго автомобиля — х км/ч, тогда скорость первого — х+10 км/ч. Второй был в пути часов, а первый — часов. Зная, что второй автомобиль был в дороге дольше на 1 час, составим и решим математическую модель:
Скорость второго автомобиля — х = 70 км/ч, скорость первого — х+10 = 70+10 = 80 км/ч
скорость первого автомобиля — 80 км/ч;скорость второго автомобиля — 70 км/ч.
Задача: При каких значения x функция принимает положительные значения.
Не есть жаренного, копченного, острого, сладкого (конфеты, шоколад), меньше соли и перца, также мучное исключить (торты, ватрушки, пирожки). хлеб есть только вчерашний , чтобы был подсушенный. порции еды уменьшить вдвое, но есть три-четыре раза в день ( т.е. завтракать и обедать обязательно), плюс утренняя или вечерняя прогулка минут 30, вот и вся диета. блюда - супы овощные, курица, говядина, телятина варенная или паренная, крупы - гречка, овсянка и т.д., больше зелени огурцы, помидоры, салат зеленый. сыры не соленные такие, как адыгейский. голодать нельзя, кушать маленькими порциями три-четыре раза в день. и еще воды побольше пить, хотя бы литр - полтора в день.
Упростить выражение:
Задача: Два автомобиля выезжают одновременно из одного города в другой, находящийся на расстоянии 560 км. Скорость первого на 10 км больше скорости второго, и поэтому первый автомобиль приезжает на место на 1 час раньше другого. Определить скорость каждого автомобиля.
Пусть скорость второго автомобиля — х км/ч, тогда скорость первого — х+10 км/ч. Второй был в пути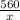 часов, а первый —
часов, а первый — 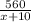 часов. Зная, что второй автомобиль был в дороге дольше на 1 час, составим и решим математическую модель:
часов. Зная, что второй автомобиль был в дороге дольше на 1 час, составим и решим математическую модель:
Скорость второго автомобиля — х = 70 км/ч, скорость первого — х+10 = 70+10 = 80 км/ч
скорость первого автомобиля — 80 км/ч;скорость второго автомобиля — 70 км/ч.Задача: При каких значения x функция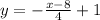 принимает положительные значения.
принимает положительные значения.
ответ: x < 12 или x ∈ (−∞; 12).