Точки A и C расположены по одну сторону от прямой, к которой от обеих точек проведены перпендикуляры AB и CD равной длины. Определи величину угла∡ABC, если ∡ADB = 47°. ∡ABC = °.

👇

Увидеть ответ

Ответ:

lolkajoin

30.01.2020

AB = CD по условию,

∠ABD = ∠CDB = 90° по условию,

BD - общая сторона для треугольников ABD и CDB, ⇒

ΔABD = ΔCDB по двум сторонам и углу между ними.

Из равнства треугольников следует, что

∠CBD = ∠ADB = 11°

∠ABC = ∠ABD - ∠CBD = 90° - 11° = 79°

Объяснение:

Точки A и C расположены по одну сторону от прямой, к которой от обеих точек проведены перпендикуляры

4,7(59 оценок)

Открыть все ответы

Ответ:

staseem35

30.01.2020

А)2Х-3У=1

3Х+У=7

УМНОЖИМ ВТОРОЕ УРАВНЕНИЕ НА (+3)

2Х-3У=1

9Х+3У=21

СКЛАДЫВАЕМ

11Х=22

Х=22\11

Х=2

ТОГДА

2Х-3У=1

2*2-3У=1

4-3У=1

-3У=1-4

-3У=-3

У=1

ответ (2,1)

Б)5Х-2У=10

-0,5Х+2У=-1

СКЛАДЫВАЕМ

4,5Х=9

Х=9\4,5

Х=2

ТОГДА

5Х-2У=10

5*2-2У=10

10-2У=10

-2У=10-10

-2У=0

У=0

ответ(2,0)

В)-4Х+3У=3

9Х-5У=9

УМНОЖИМ ПЕРВОЕ УРАВНЕНИЕ НА (+5),А ВТОРОЕ УРАВНЕНИЕ УМНОЖИМ НА (+3)

-20Х+15У=15

27Х-15У=27

СКЛАДЫВАЕМ

7Х=42

Х=42\7

Х=6

ТОГДА

-4Х+3У=3

-4*6+3У=3

-24+3У=3

3У=3+24

3У=27

У=27\3

У=9

ответ (6,9)

Задание 2

3х+2у=2,

1/2х-3у=-1/2

ПРЕОБРАЗУЕМ

3х+2у=2

0,5х-3у=-0,5

2у=2-3х

у=2-3х\2

Подстановка

0,5х-3*(2-3х\2)=-0,5

0,5х-(6-9х\2)=-0,5

0,5х-6\2+9х\2=-0,5

0,5х-3+4,5х=-0,5

5х=-0,5+3

5х=2,5

х=2,5\5

х=0,5

ТОГДА

у=2-3х\2

у=2-3*0,5\2=2-1,5\2=0,5\2=0,25

ответ ---(0,5;0,25)

Задание 3

ГРАФИЧЕСКИ

А)2х-у=0

3х+2у=14

СОСТАВЛЯЕМ ТАБЛИЦУ ДЛЯ ПЕРВОГО УРАВНЕНИЯ

2Х-У=0

2Х=У

ТАБЛИЦА

Х=0

У=0

Х=1

У=2

Х=2

У=4

Х=3

У=6

СОСТАВЛЯЕМ ТАБЛИЦУ ДЛЯ ВТОРОГО УРАВНЕНИЯ

3Х+2У=14

ТАБЛИЦА

Х=0

У=7

Х=1

У=5,5

Х=2

У=4

Х=3

У=2,5

СТРОИМ В ОДНОЙ КООРДИНАТНОЙ СИСТЕМЕ ДВА ГРАФИКА,ГДЕ ОТВЕТОМ БУДЕТ ТОЧКА ПЕРЕСЕЧЕНИЯ ЭТИХ 2Х ПРЯМЫХ

ответ(2,4)

Б) 3х-6у=5,

х/6-у/3=1.

СОСТАВЛЯЕМ ТАБЛИЦУ ДЛЯ ПЕРВОГО УРАВНЕНИЯ

3Х-6У=5

ТАБЛИЦА

Х=0

У=-5\6

Х=1

У=1\3

Х=2

У=1\6

Х=3

У=2\3

СОСТАВЛЯЕМ ТАБЛИЦУ ДЛЯ ВТОРОГО УРАВНЕНИЯ

Х\6-У\3=1

Х-2У\6=1

Х-2У=6

ТАБЛИЦА

Х=0

У=-3

Х=1

У=-2,5

Х=2

У=-2

Х=3

У=-1,5

Данная система решений не имеет (так как нет точек пересечения на графике)

Задание ПОДСТАНОВКИ

А)а) 12х-5у=7,

11х+3у=14.

3У=14-11Х

У=14-11Х\3

ПОДСТАНОВКА

12Х-5*(14-11Х\3)=7

12Х-(70-55Х\3)=7

36Х-70+55Х\3=7

91Х-70=21

91Х=21+70

91Х=91

Х=1

ТОГДА

У=14-11Х\3

У=14-11*1\3=3\3=1

ответ(1,1)

Б) 6х-9у=-11,

9х+3у=11.

3У=11-9Х

У=11-9Х\3

ТОГДА

6Х-9*(11-9Х\3)=-11

6Х-(99-81Х\3)=-11

18Х-99+81Х\3=-11

99Х-99\3=-11

99Х-99=-11*3

99Х=-33+99

99Х=66

Х=66\99=22\33

ТОГДА

У=11-9Х\3

У=11-9*22\33\3=11-6\3=5\3

ответ(22\33;5\3)

4,4(11 оценок)

Ответ:

Arturkim04

30.01.2020

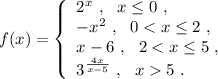
$f(x)=\left\{\begin{array}{l}2^{x}\ ,\ \ x\leq 0\ ,\\-x^2\ ,\ \ 0$

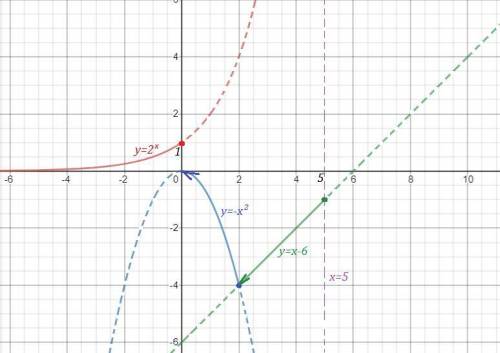
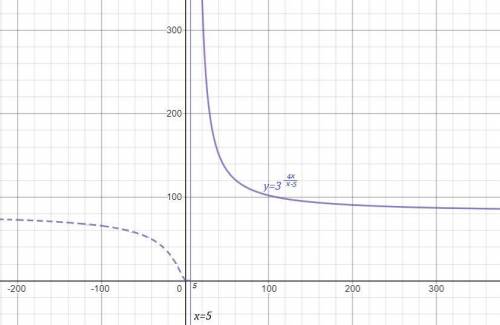
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .

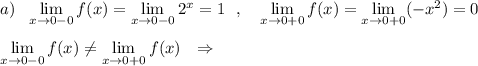
$a)\ \ \lim\limits _{x \to 0-0}f(x)=\lim\limits _{x \to 0-0}2^{x}=1\ \ ,\ \ \ \lim\limits _{x \to 0+0}f(x)=\lim\limits _{x \to 0+0}(-x^2)=0\\\\\lim\limits _{x \to 0-0}f(x)\ne \lim\limits _{x \to 0+0}f(x)\ \ \Rightarrow$

При х=0 функция имеет разрыв 1 рода .

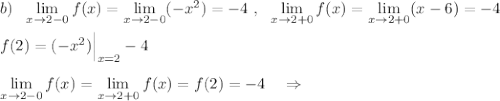
$b)\ \ \lim\limits _{x \to 2-0}f(x)=\lim\limits _{x \to 2-0}(-x^2)=-4\ ,\ \ \lim\limits _{x \to 2+0}f(x)=\lim\limits _{x \to 2+0}(x-6)=-4\\\\f(2)=(-x^2)\Big|_{x=2}-4\\\\\lim\limits _{x \to 2-0}f(x)=\lim\limits _{x \to 2+0}f(x)=f(2)=-4\ \ \ \Rightarrow$

При х=2 функция непрерывна.

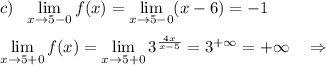
$c)\ \ \lim\limits _{x \to 5-0}f(x)=\lim\limits _{x \to 5-0}(x-6)=-1\\\\\lim\limits _{x \to 5+0}f(x)=\lim\limits _{x \to 5+0}3^{\frac{4x}{x-5}}=3^{+\infty }=+\infty \ \ \ \Rightarrow$

При х=5 функция имеет разрыв 2 рода .

График функции нарисован сплошной линией.

На 1 рисунке нет чертежа функции 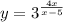$y=3^{\frac{4x}{x-5}}$ при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .