Question

СДЕЛАЙТЕ ПОЛНОСТЬЮ ВСЕ ЗАДАНИЯ!

Answer 1

$1)\ \ 3\, cosx$

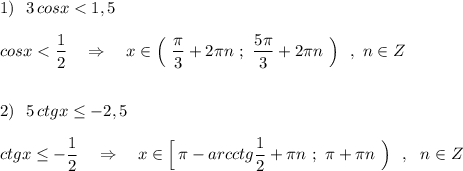
$3)\ \ cos\Big(x+\dfrac{\pi}{5}\Big)\geq \dfrac{1}{2}\\\\-\dfrac{\pi}{3}+\pi n\leq \, x+\dfrac{\pi}{5}\leq \dfrac{\pi}{3}+\pi n\ \ ,\ n\in Z\\\\x\in \Big[\ -\dfrac{8\pi }{15}+\pi n\ ;\ \dfrac{2\pi}{15}+\pi n\ \Big]\ \ ,\ n\in Z$

Answer 2

Объяснение:

1.

$3*cosx$

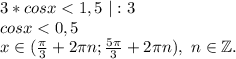
3.

$cos(x+\frac{\pi }{5})\geq \frac{1}{2} \\-\frac{\pi }{3}+2\pi n \leq x+\frac{\pi }{5} \leq \frac{\pi }{3}+2\pi n \\-\frac{8\pi }{15} +2\pi n\leq x \leq \frac{2\pi }{15} +2\pi n,\ n\in \mathbb Z.\\x\in[-\frac{8\pi }{15} +2\pi n;\frac{2\pi }{15} +2\pi n],\ n\in \mathbb Z.\\$