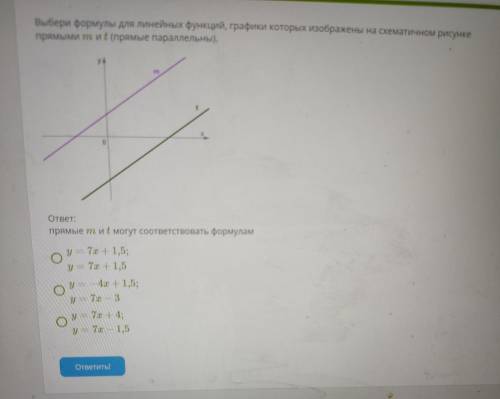
ответ: y = 7x + 4
y = 7x - 1.5
найдем точки пересечения
x^2 - 4x + 3 = 8
x^2 - 4x -5=0
х= -1 х = 5
x^2 - 12x + 35 = 8
x^2 - 12x + 27=0
х = 3 х= 9
x^2 - 4x + 3 =x^2 - 12x + 35
8х = 32
х = 4
1) интеграл от 4 до 5 (8-(x^2 - 4x + 3 ))= 8х -x^3 /3 +2x^2 -3x = 25 -125/3 +50 - 32 +64/3 -32 =11 61/3 = 31 1/3
2) интеграл от3 до 4 (8-(x^2 - 12x + 35)) = 8х - x ^3 /3 +6x^2 -35x = -27*4 -64/3 +96 +27*3 +9 -54 = 24 -21 1/3 =2 2/3
31 1/3 +3 2/3 = 35
ПРАВИЛЬНО 100%
Объяснение:1)У квадратного уравнения есть три коэффициента:
a = 1.
b = -37.
c = -27.
D = b^2 - 4ac = -37^2 - 4 * 1 * -27 = D > 0, значит у уравнения два вещественных корня (^(1/2) - это знак корня): x = (-b ± D^(1/2))/(2a).
D^(1/2) = 38,4318.
x1 = (37 + 38,4318) / (2 * 1) = 37,7159.
x2 = (37 - 38,4318 ) / (2 * 1) = -0,715879.
ответ: 37,7159, -0,715879.
2)У квадратного уравнения есть три коэффициента:
a = 1.
b = -2.
c = -9.
D = b^2 - 4ac = -2^2 - 4 * 1 * -9 = D > 0, значит у уравнения два вещественных корня (^(1/2) - это знак корня): x = (-b ± D^(1/2))/(2a).
D^(1/2) = 6,32456.
x1 = (2 + 6,32456) / (2 * 1) = 4,16228.
x2 = (2 - 6,32456 ) / (2 * 1) = -2,16228.
ответ: 4,16228, -2,16228.
3)У квадратного уравнения есть три коэффициента:
a = 2.
b = 7.
c = 6.
D = b^2 - 4ac = 7^2 - 4 * 2 * 6 = D > 0, значит у уравнения два вещественных корня (^(1/2) - это знак корня): x = (-b ± D^(1/2))/(2a).
D^(1/2) = 1.
x1 = (-7 + 1) / (2 * 2) = -1,5.
x2 = (-7 - 1 ) / (2 * 2) = -2.
ответ: -1,5, -2.
4)У квадратного уравнения есть три коэффициента:
a = 3.
b = -4.
c = -4.
D = b^2 - 4ac = -4^2 - 4 * 3 * -4 = D > 0, значит у уравнения два вещественных корня (^(1/2) - это знак корня): x = (-b ± D^(1/2))/(2a).
D^(1/2) = 8.
x1 = (4 + 8) / (2 * 3) = 2.
x2 = (4 - 8 ) / (2 * 3) = -0,666667.
ответ: 2, -0,666667.
В решении.
Объяснение:
Выбери формулы для линейных функций, графики которых изображены на схематичном рисунке прямыми (прямые параллельны).
Графики линейных функций параллельны, если k₁ = k₂, а b₁ ≠ b₂.
Соответствуют этим условиям: у = 7х + 4;
у = 7х - 1,5.