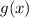;
;
и будет искомой фигурой.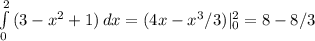
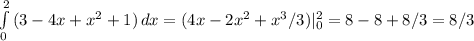
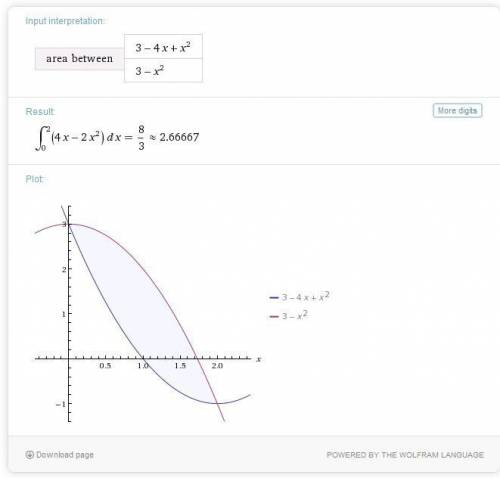
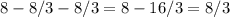(кв. ед.)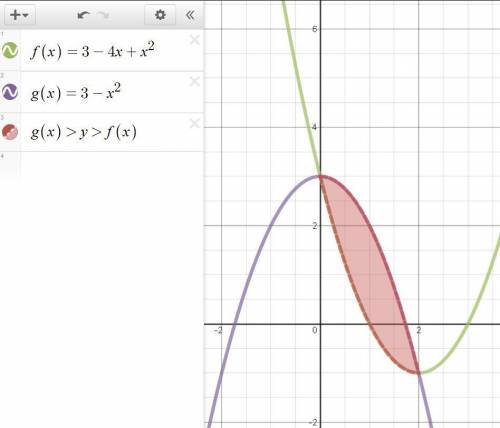
Пусть на 1 курсе студет сдал Х экзаменов, тогда на 5 курсе он сдал 4Х экзаменов.Обозначим сумму экзаменов Y₁ , Y₂ , Y₃ , которые он сдал на 2, 3 и 4 курсах через Y.
тогда Х + 4Х + Y = 25, где Х, Y ∈ Z и 1 < Х < 5, 5 ≤ Y ≤ 20
упростим 5 Х + Y = 25
Y = 25 - 5 Х
Y = 5 (5 - Х) => Y ÷ 5 => Y∈{ 5 ; 10 ; 15 ; 20}
Итак, ещё раз посмотрим, какими могут быть Х и Y:
1 < Х < 5 , Y∈{ 5 ; 10 ; 15 ; 20}.
Пусть Х=2 (1 курс) , тогда, 4Х = 8 (5 курс), тогда Y = 5 (5 - 2) = 15.
т.е. Y₁ + Y₂ + Y₃ = 15,
причем Y₁ < Y₂ < Y₃ и Y₁ , Y₂ , Y₃ больше 2 и меньше 8.
Такими числами могут быть только 3, 5 и 7.
Т.о. распределение экзаменов по курсам:
1 курс - 2
2 курс - 3
3 курс - 5
4 курс - 7
5 курс - 8
Проверка: 2 < 3 < 5 < 7 < 8 (верно)
5 курс - 8, 1 курс - 2 -> 8:2 = 4 (верно)
2 + 3 + 5 + 7 + 8 = 25 (верно)
ответ: на четвертом курсе студент сдал 7 экзаменов.
15,30,45,60,75,90-6 чисел